SPSS Special Topics: Lineare Regression
Michael Wiseman
Inhalt
- Einführung
- 1. Einfache lineare Regression
- 2. Multiple lineare Regression
- 3. Binäre logistische Regression
- Übungen
- Literatur
Einführung
Die Schriftreihe Special Topics entstand aus dem Wunsch mehrerer Teilnehmer am LRZ-Einführungskurs SPSS für Windows (siehe [1]) nach weiteren Informationen, die über die reine Bedienung des Programms hinausgehen. Auch die Themen wurden durch Kunden des LRZ bestimmt, die unsere Spezialisten im Bereich der angewandten Statistik konsultiert haben: Diese Reihe versucht, Informationen zu dort häufig aufkommenden Missverständnissen und Fragen zu geben; aber auch, wie in der vorliegenden Schrift, bestimmte Themenbereichte etwas näher zu betrachten.
Diese Schrift geht davon aus, dass Sie Kenntnisse sowohl der Grundbegriffe der Statistik, als auch der Steuerung von SPSS unter Windows besitzen.
Datenbestände für die Übungen und Beispiele
Unter dem Begriff Datenbestände für die Übungen und Beispiele befinden sich alle in dieser Schrift angesprochenen Dateien: Klicken Sie mit der rechten Maustaste den gewünschten Dateinamen an, wählen Sie die Option Verknüpfung speichern unter ... und speichern Sie die gewählte Übungsdatei lokal ab!
1. Einfache lineare Regression
Sinn der einfachen Regression ist es, die Abhängigkeit einer Variablen von einer zweiten zu untersuchen. Das Modell setzt intervallskalierte, normalverteilte Variablen voraus.
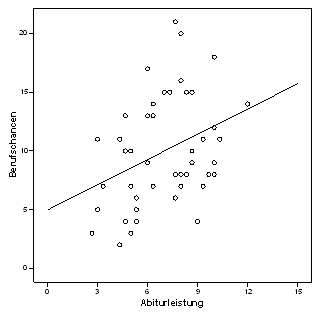
Als Beispiel nehmen wir an, dass die Leitung einer Privatschule die zu erwartende Abiturleistung von Kandidaten für die 5. Klasse schätzen will, um möglichst viele akademisch vielversprechende Kinder aufzunehmen. Diese zu erwartende Abiturleistung will die Schulleitung anhand der Antworten auf Fragen eines einfachen Fragebogens schätzen, der die von den Schülern erwarteten Berufschancen quantifiziert.
Zunächst wird eine Stichprobe von Grundschülern genommen und diese Schätzung der künftigen Berufschancen gemessen, die die Kinder für sich selbst erwarten. Einige Jahre später steht die tatsächliche mittlere Abiturleistung derselben Schüler in den Kernfächern Deutsch, Englisch und Mathematik zur Verfügung. Es wird eine Regression durchgeführt, um die Abhängigkeit der Abiturleistung von den Berufserwartungen zu untersuchen und in Form einer Gleichung zu quantifizieren.
Bei einer gelungenen Analyse beabsichtigt die Schulleitung, bei Neubewerbern die Berufserwartungen zu messen. Die Regressionsgleichung wird dann angewendet, um eine Schätzung der späteren Abiturleistung eines jeden Kindes zu berechnen. Kinder mit einer zu erwartenden Abiturleistung von mehr als 7 werden in der Schule aufgenommen, die restlichen abgelehnt.
Grafische Darstellung der Regressionsgerade
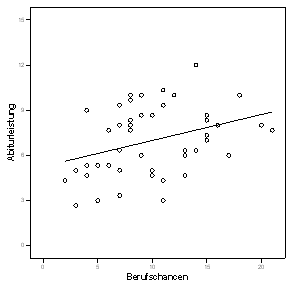
Starten Sie SPSS mit der Datendatei data_reg.sav ! Über Grafiken + Streudiagramm ... wählen Sie Einfach aus und definieren Sie als Y-Achse die Variable leistung (den arithmetischen Mittelwert der Kernfächernoten), als X-Achse die Variablen chancen (die Schätzung der Berufschancen). Im Diagrammeditor klicken Sie einen der kleinen Kreise an, um die Punktwolke zu markieren, über die rechte Maustaste selektieren Sie "Hinzufügen Anpassungslinie bei Gesamtwert", und wählen Sie "linear" aus. Ändern Sie anschließend die Achsenbeschriftung der Y-Achse, um das Diagramm (Abb. 1.1) zu erhalten:
Abb. 1.1 Eine Punktwolke und ihre Regressionsgerade
Mathematische Darstellung der Regressionsgerade
Diese Gerade zeigt die Schulleistung in Abhängigkeit von den erwarteten Berufschancen. Je höher die Berufserwartungen, desto höher tendiert auch die Leistung zu sein. Eine solche Gerade nennt man die "lineare Regression der Berufschancen auf die Leistung".
Das zugrundegelegte Modell
y = c + bx + e (Gl. 1.1)
besagt, dass die Variable y linear von der Variablen x abhängt: c ist eine Konstante (der Schnittpunkt zwischen der angepassten Gerade und dem Null-Punkt der X-Achse), b der Grad der Steigung der Gerade, e die Abweichung des beobachteten (x, y)-Punktes in der y-Richtung von der Gerade. Die Gerade wird so positioniert, dass die Quadratsumme dieser Abweichungen minimiert wird (Mindestquadrat-Verfahren): Große Abweichungen tragen dementsprechend besonders stark zu der Positionierung der Gerade bei. Die y-Variable wird allgemein als abhängige (oder Ziel-)Variablen bezeichnet, die x-Variable als unabhängige oder Prädiktorvariablen. In unserem Beispiel ist y die Abiturleistung, x die erwarteten Berufschancen: Die Abhängigkeit der Zielvariablen "Abiturleistung" vom Prädiktor "Berufschancen" wird durch die Regression untersucht und quantifiziert.
Es wird angenommen, dass die y-Variable keine perfekten, mathematisch exakten Werte enthält: Der Fehlerausdruck e spiegelt diese Annahme wider. Die x-Variable dagegen wird als mathematisch exakt (das heißt: frei von Mess- oder anderen Fehlern) behandelt ? eine Annahme die zwar bei fast allen Anwendungen dieses Modells nicht erfüllt wird, die aber trotzdem oft gerechtfertigt werden kann. Beispiel: Die Größe eines Menschen in Millimeter gemessen ist sicherlich für die meisten Anwendungen präzis genug, dass man ohne Bedenken das Regressionsmodell anpassen könnte.
Die SPSS-Regressionsprozedur liefert die Modellparameter
Die Parameter zur Gerade erhält man durch den Aufruf Analysieren + Regression + Linear (Abb. 1.2):
Abb. 1.2 SPSS-Steuerungsfenster für die lineare Regression
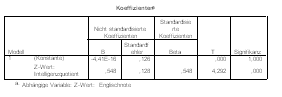
In das Feld Abhängige Variable übertragen Sie den Variablennamen leistung, in das Feld Unabhängige Variable(n) den Variablennamen chancen. Wir wollen also untersuchen, inwieweit die Abiturleistung von den erwarteten Berufschancen vorhergesagt werden kann. Die Tabelle Koeffizienten (Tab. 1.1) der SPSS-Ausgabe
Tab. 1.1 Die Parameter des angepassten linearen Modells

enthält unter anderem die nicht-standardisierten B-Koeffizienten, mit denen diese "beste" Schätzung der Abiturleistung auf der Basis der Variablen chancen berechnet werden können:
leistung = 5,262 + 0,173 × chancen (Gl. 1.2)
Diese Gleichung beschreibt die gerade Linie von Abb 1.1: der Wert 5,262 (die Konstante) ist der Schnittpunkt zwischen der Regressionslinie und dem Null-Punkt der Y-Achse. Der Wert 0,173 (der B-Koeffizient) quantifiziert die Steigung der angepassten Regressionsgerade und kann demnach wie folgt interpretiert werden: Ändert sich der Wert für chancen um einen Punkt, so verändert sich der Wert für leistung um 0,173 Punkte. Solche B-Koeffizienten werden also zur Gewichtung der rohen unabhängigen Variablen ? hier: chancen ? angewendet, um (zusammen mit der Konstante) die Schätzung der abhängigen Variablen ? hier: leistung ? durchzuführen.
Als Beispiel nehmen wir ein Kind, das ein Testergebnis von chancen = 4 geliefert hätte. Die obige Regressionsgleichung würde seine Abiturleistung als
5,262 + 0,173 × 4 = 5,954 (Gl. 1.3)
oder (rund) 6 Punkte schätzen.
Einfluß der Mess-Skala der Prädiktoren
Die Werte des B-Koeffizienten und die Werte der unabhängigen Variablen hängen also unmittelbar miteinander zusammen: Ändert man die Skalierung der Variablen, so muss sich zwangsläufig auch dieser Koeffizient mitverändern. Generieren Sie mittels Transformieren + Berechnen... eine neue Variablen xchancen, die um ein Faktor 10 kleiner ist als chancen:
xchancen = chancen / 10 . (Gl. 1.4)
Wiederholen Sie nun die Regressionsanalyse, wobei Sie chancen durch xchancen ersetzen! Beobachten sie den B-Koeffizienten! Vergleichen Sie die Beta-Koeffizienten der beiden Regressionen! Der Beta-Koeffizient (hier unverändert 0,352) ist eine standardisierte Version des B-Koeffizienten, die von der Messeinheit der Variablen unabhängig ist: Dieser Wert bleibt demnach durch die Skalierung der Variablen chancen (die wir als xchancen generiert haben) unverändert.
(Da der Beta-Koeffizient unabhängig von den Messeinheiten einzelner Prädiktoren ist, wird er hauptsächlich zum Vergleich zwischen verschiedenen Prädiktoren herangezogen: Je höher der Beta-Koeffizient, desto mehr trägt der entsprechende Prädiktor zur Vorhersage bei. Dies wird später unter der Rubrik "Multiple Regression" näher diskutiert.)
Vorsicht vor Missbrauch des Regressionsmodells!
Statistische Modelle sind stets eine Vereinfachung ? oft eine grobe Vereinfachung ? der tatsächlichen Daten. Die Grafik zu unserem Beispiel verdeutlicht, dass dies auch hier der Fall ist: Einzelne Punkte (Schüler) liegen weit von der Gerade entfernt, lediglich ein einziger Punkt liegt darauf. Das heißt: Die Gleichung liefert für einzelne Personen keine präzise Schätzung ihrer späteren Abiturleistung. Sie liefert sehr wohl die im Sinne der Mindestquadratkriteriums "beste" Schätzung über die Gesamtheit der Gruppe betrachtet, versagt aber typischerweise bei Einzelbeobachtungen.
Im Allgemeinen gilt: Je weniger die Streuung der Punkte um die geschätzte Gerade, desto geeigneter ist das Regressionsmodell; je größer die Streuung, desto ungeeigneter, insbesondere bei einzelnen Personen.
Beispiel einer möglichen Fehlanwendung
Als Beispiel betrachten wir wieder den Wert chancen = 4 (siehe die untenstehende Grafik Abb. 1.3). Drei Werte der Variablen leistung für Schüler mit diesem Wert wurden beobachtet: 4,67, 5,33 und 9,00. Nach der Gleichung wäre die geschätzte Abiturnote bei chancen = 4 wie oben berechnet rund 6 ? ein Wert, der den Daten von keiner einzigen Person mit dem Testergebnis chancen = 4entspricht (sortieren Sie den Datenbestand nach der Variablen chancen und bestätigen Sie diese Behauptung!). Bei zwei beobachteten Werten ist der geschätzte Wert zwar unpräzis aber vielleicht akzeptabel; bei einem (leistung = 9) ist er gänzlich unbrauchbar.
Die Regression wird aber oft genau dafür benutzt, dass auf der Basis einer solchen Gleichung anhand einer tatsächlich gemessenen Variablen der Wert einer nicht beobachteten Variablen geschätzt wird: In unserem Beispiel war dies sogar das erklärte Ziel der Studie ? die erwarteten Berufschancen bei einer neuen Gruppe von Grundschulkindern zu messen, deren Abiturleistung natürlich noch nicht vorliegt, um genau diese Leistung vorauszusagen. Das Problem wird dadurch exacerbiert, dass die Regressionsgerade auf der Basis einer bestimmten Stichprobe geschätzt, die Anwendung jedoch bei ganz anderen Personen durchgeführt wird, sodass die Güte der angewendeten Gerade zwangsläufig noch weiter vermindert wird. Inwieweit eine solche Anwendung verantwortlich ist, muss jeder für sich selbst entscheiden.
Abb. 1.3 Vorhersage durch Anwendung einer Regressionsgerade
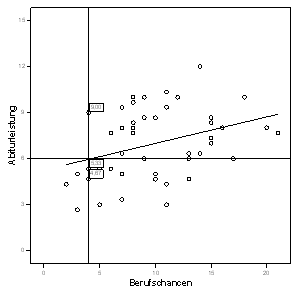
Aus Sicht der Schule würde man trotz der schwachen Güte dieser Vorhersage das Ziel zumindest teilweise erreichen: Im Schnitt würde die Schule durch die Anwendung dieser Gerade mehr akademisch begabte Kinder akzeptieren als ohne. Die Schulleitung beabsichtigt ja, die Gerade zu benutzen, um nur die Kinder aufzunehmen, von denen eine Abiturleistung von mehr als sieben Punkten zu erwarten ist. Setzen wir diesen Wert 7 in der Gleichung ein:
chancen = (7 ? 5,262) / 0,173 = 10,046 . (Gl. 1.5)
Da nur ganzzählige Punktzahlen bei diesem Berufstest möglich sind, entscheidet sich die Schule, Kinder mit 10 Punkten oder mehr bei der Variablen chancen zu akzeptieren.
Jedes Kreischen im Diagramm (Abb. 1.3) stellt die (x, y)-Position einer oder mehrere Kinder dar: Tabelle 1.2 enthält die zu unserem Beispiel relevanten Zahlen: 15 Kinder erreichten tatsächlich eine Abiturleistung über 7 und wurden von der Regressionsanalyse auch korrekt klassifiziert. Die Schule hätte aber auch 11 Kinder akzeptiert, die mehr als 10 Punkte bei dem Berufstest, jedoch weniger als sieben Punkte bei der Abiturleistung erreichten: Die Klassifikation dieser Kinder durch die einfache Regressionsgerade ist falsch und führt zur Aufnahme doch nicht geeigneter Kinder. 14 Kinder hätte die Schule nicht akzeptiert, diese jedoch haben aber tatsächlich das Kriterium erreicht. Insgesamt wurden 15 + 13 = 28 Kinder korrekt, die anderen 11 + 14 = 25 falsch klassifiziert: 28:25 ist keine besonders gute Erfolgsquote!
Im Schnitt gewinnt die Schule trotzdem: Sie hätte zwar einige Schüler verloren, die die Zielleistung doch erreicht haben, und andere akzeptiert, die die Leistung nicht bringen konnten; aber 28:25 bleibt (auch wenn nur marginal) doch besser als 50:50. Vom Standpunkt des einzelnen Kindes jedoch kann eine Anwendung dieser Art katastrophale Folgen haben. Die Entscheidung, eine solche Anwendung in der reellen Welt zu benutzen, ist nicht einfach.
Die Güte einer solchen Vorhersage wird oft durch Trefferquoten quantifiziert, die man anhand einer 2 × 2 Tabelle (Tab 1.2) darstellen kann. Anhand unseres Beispiels:
Tab. 1.2 Trefferquoten-Tabelle
|
|
Beobachtete Abi-Note |
|
|
Vorhergesagte Abi-Note |
> 7 |
<= 7 |
|
> 7 |
15 |
11 |
|
<= 7 |
14 |
13 |
Hieraus werden zusammenfassende Statistiken berechnet:
- Sensitivität: aus allen positiven Fälle, die Proportion Positive (tatsächliche Abi-Note > 7):
15 / (15 + 14) = 0,517 - Spezifizität: aus allen negativen (tatsächliche Abi-Note <= 7) Fällen, die Proportion korrekt vorhergesagte::
13 / (13 + 11) = 0,542 - Positiver Wahrscheinlichkeitswert: die Proportion der Fälle, die als positiv vorhergesagt wurden und tatsächlich positiv waren (beobachtete Abi-Note > 7,0):
15 / (15 + 11) = 0,577
Dies ist der Wert, der die Schule interessiert: 57,7% der laut der Gleichung vielversprechenden Schüler erreichten tatsächlich eine Abi-Note über 7. - Negativer Wahrscheinlichkeitswert: die Proportion der Fälle, die als negativ (Note <= 7,0) vorhergesagt wurden und in der Tat negativ waren:
13 / (14 + 13) = 0,481
Alle vier Werte werden oft als Prozente ausgedrückt, die Sensitivität in unserem Beispiel etwa als 53,6%.
Ein Bisschen zu viel des Guten vielleicht, aber diese sind oft benutzte und daher für den Studierenden wichtige Begriffe.
Güte der Anpassung des Modells an vorhandenen Daten
Wie gut erklärt diese Gleichung die beobachteten Daten? Entscheidungshilfen zur Akzeptanz des Modells liefert SPSS. Die erste, naïve Frage ist die nach der Signifikanz. Hier lautet diese Frage: Ist die Steigung der Gerade signifikant unterschiedlich von Null? (Präziser: können wir durch die Gerade signifikant mehr Varianz der Variablen chancen erklären als ohne die Gerade?) Falls nicht, dann kann man anhand der x-Variablen nichts über die y-Variablen aussagen. Unsere frühere Tabelle (Tab. 1.1) lieferte für chancen die Statistik T = 2,464, p <= 0,05. Das heißt: Wir können mit den erwarteten Berufschancen signifikant (mit 95% Sicherheit) mehr als gar nichts über die Schulleistung vorhersagen. Dieser Wert testet aber lediglich, ob die Steigung der Gerade unterschiedlich Null ist; er sagt nichts über die Güte der Anpassung aus ? und auch nichts über die inhaltlich meist interessantere Frage, ob eine so geringe Steigung überhaupt von praktischem Interesse sein kann. Und noch eine Gefahr: Je größer die Stichprobe, desto geringer darf die Steigung sein und trotzdem Signifikanz erreichen (siehe dazu die Diskussion zum Thema Signifikanz und Relevanz in [2]).
Tabelle (Tab. 1.3) enthält mehr Informationen zur Güte der Regression:
Tab. 1.3 Güte der Anpassung des Modells

Traditionsgemäß wird die Statistik R2 für die Güte einer Regressionsgleichung herangezogen: Sie stellt die Proportion der beobachteten Varianz dar, die durch die Gleichung erklärt werden kann: Hier also 0,124. In diesem Fall heißt das: Lediglich rund 12,4% (R2 × 100) der Varianz von leistung kann durch chancen erklärt werden ? oder aber: (100 ? 12,4) = 87,6% der Varianz der Variablen leistung kann nicht durch unsere Gerade erklärt werden.. Die Statistik R2 wird auch "Bestimmtheitsmaß" genannt, denn sie quantifiziert wie gut die abhängige Variable durch den Prädiktor bestimmt werden kann. Der Wert von R2 wird auf der Basis der vorhandenen Stichprobe gerechnet und ist eine überoptimistische Schätzung des Populationswertes; die korrigierte Version (Korrigiertes R-Quadrat) ist ein realistischerer Wert, der die Tatsache berücksichtigt, dass die Regressionsgerade anhand einer bestimmten Stichprobe angepasst wurde, die Anpassung jedoch für eine gänzlich andere Stichprobe benutzt wird.
In diesem einfachen Fall, wo lediglich zwei Variablen untersucht werden, enthält die restliche Ausgabe redundante Information: R ist identisch mit dem einfachen Korrelationskoeffizienten zwischen leistung und chancen. Der Standardfehler des Schätzers quantifiziert die Güte der Schätzung durch einen (standardisierten) Vergleich zwischen den beobachteten Werten y und den anhand der Gleichung geschätzten Werten y*. Der hohe Wert dieses Fehlerausdrucks im Beispiel spiegelt die relativ breite Streuung, die in der Grafik schon erkennbar war, sowie die entsprechend schwache Vorhersagekraft der Gleichung wider, die die statistische Analyse ergibt.
Auch die ANOVA-Tabelle (Tab. 1.4)
Tab. 1.4 ANOVA-Tabelle zur Signifikanz der Regressionsgerade
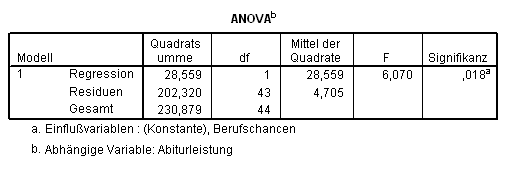
enthält in diesem einfachen Fall redundante Informationen, fasst aber das Anpassen des Modells schön zusammen. Die Quadratsummen spiegeln die jeweiligen Varianzen wider. Berechnet man zum Beispiel das Verhältnis der Regressionssumme zur Gesamtsumme (Gesamt), so erhält man genau den Wert des R2: 28,559 / 230,879 = 0,124. Residuen quantifiziert den Anteil der Varianz, der durch die Regression nicht erklärt werden kann:
202,320 / 230,879 = 0,876 = 1 ? 0,124 . (Gl. 1.5)
Den F-Wert erhält man wie üblich durch Quadrierung des entsprechenden T-Werts (aus der Tabelle Koeffizienten, Tab 1.1 weiter oben).
Güte der Anpassung für Einzelfälle
Diese Überlegungen zur Regression verdeutlichen ein Grundproblem der angewandten Statistik: Für eine Gruppe als Gesamtheit betrachtet können Ergebnisse durchaus Gültigkeit besitzen, für ein Individuum jedoch sehr falsch liegen. Dies ist besonders in den Bereichen von großer Bedeutung, wo unsere Entscheidungen das Schicksal von Menschen betreffen: Medizin, Psychologie, Berufsberatung, . . . Schon die Grafik zu unserer Regression zeigt, dass mehrere Individuen weit von der Gerade liegen. Für die gesamte Gruppe von Kindern dürfen wir den Schluß ziehen, dass je besser die erwarteten Berufschancen, desto besser im Schnitt die Leistung ? ein durchaus interessantes Ergebnis. Würden wir das Modell jedoch dazu missbrauchen, einen einzelnen Schüler auf der Basis seiner pessimistischen Berufserwartungen als akademisch unbegabt abzustempeln, so würden wir einen unverantwortlichen Fehler machen.
Im Falle der Regression gibt SPSS eine für die Interpretation sehr wichtige Liste genau dieser Einzelpersonen aus. Eine Liste aller Fälle erhalten Sie über Analysieren + Regression + Linear + Statistiken. . . und dann unter Residuen die Auswahl Fallweise Diagnose und Alle Fälle: Es wird für jeden einzelnen analysierten Fall eine Zeile ausgegeben. Die folgende Tabelle (Tab. 1.5) enthält die ersten 25 Fälle aus unserem Beispiel.
Die Spalten:
Fall Nummer entspricht der grauen, linken Spalte des SPSS-Dateneditorfensters;
Abiturleistung enthält die tatsächlich beobachteten Werte der Variablen leistung;
Nicht standardisierter vorhergesagter Wert ist der mittels der Regressionsgerade geschätzte Wert der Variablen leistung;
Nicht standardisierte Residuen ist der Unterschied zwischen dem beobachteten und dem geschätzten Wert;
Standardisierte Residuen ist Nicht standardisierte Residuen in standardisierter Form, das heißt in Standardabweichungen ausgedrückt;
Status zeigt an, ob der Fall fehlende Werte aufwies; M (englisch: "missing") kennzeichnet fehlende Werte.
Tab. 1.5 Fallweise Diagnostische Werte
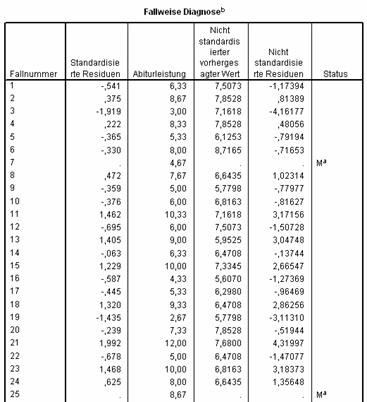
Hier sieht man wie gut ? oder schlecht ? die Schätzungen bei einzelnen Schülern sind. Bei Fall Nummer 14 ist die Vorhersage (6,47) sehr gut: Der tatsächlich gemessene Wert war 6,33. Bei Fall 21 dagegen ist die Vorhersage extrem unpräzis.
Residualwerte: Was hat das Modell nicht erklären können?
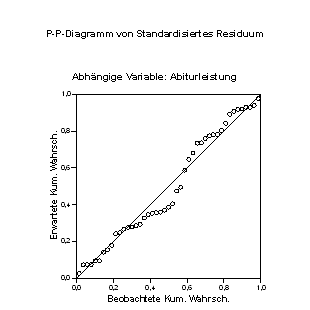
Wie gut das Modell für einen bestimmten Datensatz ist, hängt nur teilweise davon ab, wie groß die Streuung der einzelnen Punkte um die Gerade ist. Eine Annahme des Modells betrifft die Normalität vor allem der Residuen (y ? y*), wobei y die beobachteten, y* die vorhergesagten Werte sind. Als erstes betrachten wir die Normalverteilungsdiagramm dieser Residuen: Über Analysieren + Regression + Linear. . . definieren sie die Regressionsgerade von vorhin, drucken Sie nun den Knopf Diagramme. . . und wählen Sie (ohne weitere Angabe) Normalverteilungsdiagramm aus: Das Ergebnis (Abb. 1.4) zeigt die Abweichung dieser Residualwerte (die kleinen Kreise) von der perfekten Normalität (der geraden Linie). In unserem Falle scheinen Werte um den Wert 0,50 von der Normalität etwas abzuweichen:
Abb. 1.4 Grafik der standardisierten Residuen
Weitere Informationen zu den Residuen
Über Analysieren + Regression + Linear. . . definieren sie die Regressionsgerade von vorhin, betätigen Sie aber den Knopf Speichern..., um folgendes Fenster (Abb. 1.5) zu erhalten:
Abb. 1.5 SPSS-Steuerungsfenster zur fallweisen Speicherung der vorhergesagten Werte
Hier können pro Fall einige Werte berechnet und gespeichert werden, die zur Diagnose des Modells benutzt werden können. Wählen Sie unter Vorhergesagte Werte und Nicht standardisiert (das heißt: Die Werte sind im gleichen Maßstab wie die beobachteten Rohwerte) und unter Residuen, Standardisiert aus. Führen Sie die Analyse durch.
Der Datensatz enthält nun zwei neue Variablen: PRE_1 (die geschätzten Werte y*) und ZRE_1 (die standardisierten Residuen y-y*) normiert zu Standardabweichung 1, Mittelwert 0. Eine Zusammenfassung der Residuen wird auch als letzte Tabelle der Ausgabe ausgegeben (Tab. 1.6):
Tab. 1.6 Statisken zur Residuen
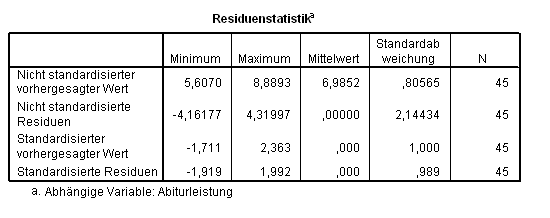
Die letzte Zeile Standardisierte Residuen zeigt in Standardabweichungseinheiten die extremsten Abweichungen zwischen den beobachteten und den geschätzten Werten an. Die schlechtetesten Schätzungen liegen also knapp zwei Standardabweichungen von den beobachteten Werten entfernt.
Grafische Darstellung der Anpassung
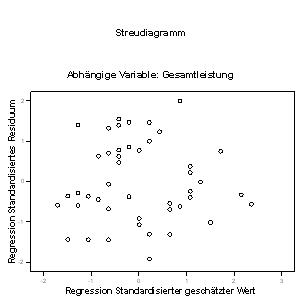
Dies können wir auch grafisch darstellen. Wiederholen Sie den Aufruf zur linearen Regression, klicken Sie Diagramme? Als Y-Achse mit der Variablen ZRESID (den standisierten Residuen y ? y*), die X-Achse mit ZPRED (dem standardisierten Prädiktor).
Zunächst ist die resultierende Grafik (Abb. 1.6) in der Hinsicht zufriedenstellend, dass alle Punkte in einer waagerechten Lage um die Null-Linie liegen. Es ist sonst kein Muster zu erkennen. Zweitens aber sollte man Ausschau auf Extremwerte halten ? einzelne Werte, die deutlich außerhalb des Rahmens der restlichen Punkte liegen. Weichen solche Werte wirklich extrem von den anderen ab, so könnte man erwähnen, die Regressionsanalyse ohne diese Fälle zu wiederholen. (Einzelne Fälle können über den Diagrammeditor identifiziert werden: Klicken sie einen Punkt in der Punktwolke an und wählen Sie Diagramme + Datenbeschriftungen einblenden.)
Auch die Grafik der Residuen mit der unabhängigen Variablen sollte inspiziert werden. Wiederholen Sie den Vorgang, definieren Sie jedoch die Y-Achse als *ZRESID. Solche Untersuchungen der Residuen sind wichtig, um festzustellen, ob die Voraussetzungen (die Normalverteilung der Residuen) für die Regression zufriedenstellend erfüllt sind.
Abb. 1.6 Grafische Darstellung der Residuen
Asymmetrie der Regression
Zeichnen Sie die umgekehrte Regression, nämlich die Regression von der Leistung auf Berufschancen; berechnen Sie die Statistiken dazu und vergleichen Sie die beiden Ergebnisse!
Folgende Grafik (Abb. 1.7) im Vergleich zu Abb. 1.1 verdeutlicht: Im allgemeinen ist die Regression von X auf Y nicht gleich die von Y auf X. Welche Variante man nimmt, hängt von der Fragestellung ab. Die einfache Regression testet die Frage, ob eine Variable (traditionsgemäß die, die in der Y-Achse dargestellt ist) von einer anderen Variablen abhängt ? oder, etwas präziser ausgedrückt: Wenn man eine Variable gemessen hat, in wie fern kann man den Wert einer zweiten Variablen bestimmen?
Beispiel: Es ist wahrscheinlich uninteressant zu fragen, ob anhand des Grades der Verfärbung der Leber die tägliche Alkoholeinnahme bestimmt werden kann. Anders herum könnte die Frage durchaus interessant sein.
Abb. 1.7 Regression nach Tausch des Prädiktors mit der abhängigen Variablen
Es ist verlockend, die Regression als eine Art kausalen Zusammenhang zwischen zwei Variablen zu betrachten. Aber ein statistischer Zusammenhang impliziert keine Kausalität, obwohl er diese natürlich nicht auschließt. Unser Beispiel verdeutlicht dies: Die Abiturleistung wird nicht unbedingt von den Erwartungen der Berufschancen verursacht. Möchte man diese (nicht ganz abwegige) Hypothese doch testen, so müsste man eine gezielt dafür entworfene Studie durchführen.
Ausreißer
Das schon besprochene Mindestquadrat-Verfahren sorgt dafür, dass je weiter ein Punkt von der Regressionslinie entfernt liegt, desto stärker trägt dieser Punkt zu der Bestimmung dieser Gerade bei. Werte, die für die gesamte Datenmenge untypisch sind, werden als ?Ausreißer? bezeichnet. Sie stellen in der gesamten Statistik ?insbesondere aber im Falle der Regression ? ein Problem dar.
Die folgende Grafik (Abb. 1.8) zeigt eine leicht zu interpretierende Regressionslinie auf der Basis von 50 Datenpunkten:
Abb. 1.8 Eine Regressionslinie zu Beobachtungen ohne Ausreißer
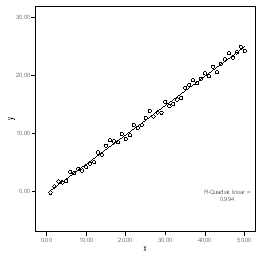
Der Eindruck dieser Grafik wird durch die Regressionsanalyse bestätigt: Die Regressionsgerade liefert einen korrigierten R2-Wert von 0,994 und fasst somit diese Daten sehr gut zusammen (Tab. 1.7):
Tab. 1.7 Regressionskoeffizienten zur Regressionslinie ohne Ausreißer

y = 0,508x - 0,364 . (Gl. 1.6)
Wir fügen zu dieser Datenmenge einen zwar krassen, aber einzigen Ausreißer hinzu (unten rechts in der Abb. 1.9):
Abb 1.9 Veränderte Regressionslinie durch Hinzufügen eines einzigen Ausreißers ( 51, -9)
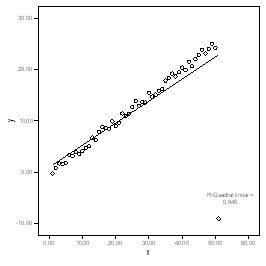
Die Gleichung (Tab. 1.8, Gl. 1.7)) ändert sich merklich ...
Tab. 1.8 Veränderte Gleichung durch Hinzufügen eines Ausreißers
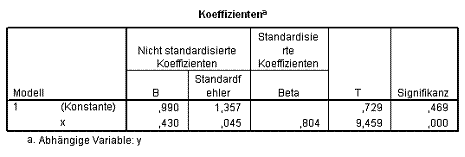
y = 0,99 + 0,43x . (Gl. 1.7)
... und der korrigierte R2-Wert reduziert sich erheblich auf 0,639.
In diesem künstlichen Fall ist die Sache klar: Der Punkt unten rechts in der Grafik (Abb. 1.9) ist ein klassischer Ausreißer und der Fall, der diese Daten lieferte, sollte aus der Regressionsanalyse ausgeschlossen sein.
In typischen Fällen ist die Lage nicht so deutlich. Da einzelne Fälle einen großen Einfluss sowohl auf die Positionierung der Gerade als auch auf die Güte der Anpassung haben können, ist es verlockend, alle Fälle auszuschließen, die die Anpassung stören. Dieser Vorgang wäre selbstverständlich unzulässig.
Die gerade besprochenen diagnostische Ausgaben von SPSS helfen zwar bei der Identifizierung solcher Ausreißer, aber die Entscheidung, ob ein Fall aus der Gleichung entfernt werden darf, liegt ausschließlich bei dem Anwender. Und letztendlich können nur inhaltliche (zum Beispiel medizinische) Überlegungen diese Entscheidung rechtfertigen.
Regression versus Korrelation
Zunächst wählen Sie über Daten + Fälle auswählen? nur die Fälle aus, die vollständige Datensätze bezüglich englisch und iq geliefert haben: dies geschieht über die Funktion not(missing(englisch)) & not(missing(iq)).
Eigentlich scheint der Unterschied zwischen Korrelation und Regression klar: Korrelation ist symmetrisch ? der Korrelationskoeffizient zwischen englisch und iq und der zwischen iq und englisch sind identisch.
Übung:
Berechnen Sie diesen Korrelationskoeffizienten!
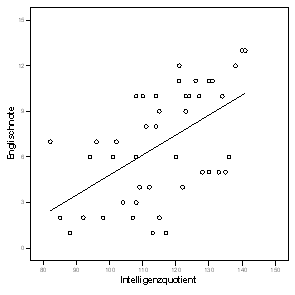
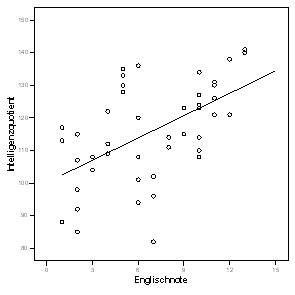
Regression ist dagegen asymmetrisch. Die Regression von englisch auf iq unterscheidet sich von der Regression von iq auf englisch. Folgende Grafik (Abb. 1.10) verdeutlicht dies:
Abb. 1.10 Asymetrie der Regression
|
|
|
Übung:
Berechnen Sie beide lineare Regressionen zu dieser Grafik (Tab. 1.9)!
Tab. 1.9 Asymetrie der Regression
|
|
|
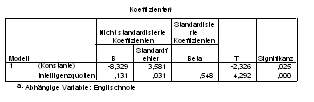
Diese Gleichungen unterscheiden sich natürlich:
englisch = -8,329 + 0,131 × iq (Gl. 1.8)
iq = 100,165 + 2,282 × englisch . (Gl. 1.9)
Der Beta-Koeffizient ist jedoch bei beiden Gleichungen identisch (0,548) ? und ist zudem in diesem Fall mit lediglich einem Prädiktor auch identisch mit dem Korrelationskoeffizienten.
Diese Tatsache, dass der Beta- und der Korrelationskoeffizient bei einer einfachen Regression identisch sind, sorgt oft für Verwirrung: Ist nun die Regression asymmetrisch oder nicht? Um dies zu verstehen, muss man die Auswirkungen des Vorgangs "Standardisieren" begreifen:
Über Analysieren + Deskriptive Statistiken + (noch einmal) Deskriptive Statistiken... kreieren wir standardisierte Varianten der Variablen englisch und iq (Abb. 1.11):
Abb. 1.11 SPSS-Steuerungsfenster zum Erzeugen standisierter Variablen

Diese neuen Variablen werden automatisch Zenglisch und Ziq benannt und erscheinen wie üblich am rechten Ende (in der Datenansicht) oder am unteren Ende (in der Variablenansicht) des Dateneditorfensters. Standardisierte Variablen haben Mittelwert Null und Varianz 1.
Übung:
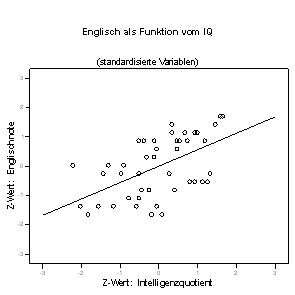
Wiederholen Sie die Regressionsanalysen einschließlich grafischer Darstellung, benutzen Sie dabei aber die standardisierten Variablen Zenglisc und Ziq!
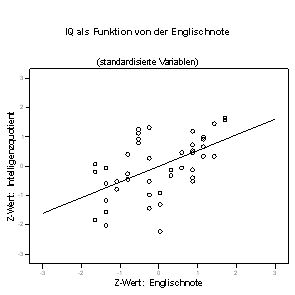
Abb. 1.12 Symmetrische Regressionsgeraden bei standardisierten Variablen
|
|
|
Der visuelle Eindruck (Abb. 1.12), durch Standardisierung verschwinde der Unterschied zwischen den Regressionslinien, wird durch die statistische Analyse (Tab. 1.10) bestätigt:
Tab. 1.10 Symmetrische Regressionsgeraden bei standardisierten Variablen
|
|
|
Die bisherige, bei den nicht standardisierten Variablen beobachtete Asymmetrie der Regressionslinien wird allein durch die Streuung der Variablen verursacht. Weisen also beide Variablen die gleiche Streuung auf (wie bei standardisierten Variablen der Fall), so gibt es natürlich keine Asymmetrie mehr. Da auch beide Mittelwerte gleich Null sind, ist die Konstante bei beiden Gleichungen zwangsläufig auch Null (die ausgegebenen Werte sind in wissenschaftlicher Notation, sodass z.B. die Konstante 7,235E-16 einfach 7,235 × 10-16 bedeutet ? Null also, mit winzigen numerischen Rundungsfehlern erst ab der 15. Nachkommastelle). Beide Regressionslinien sind bei standardisierten Variablen identisch.
Solche Normierungen ändern inhaltlich nichts an der Interpretation ? es ist völlig egal, ob wir die Konventionen der T- (Mittelwert 50, Standardabweichung 10), der IQ- (Mittelwert 100, Standardabweichung 15) ? oder aber die normierte Skalierung mit Mittelwert 0 und Standardabweichung 1 benutzen. Ein Wert eine Standardabweichung oberhalb des Mittelwerts bleibt unverändert eine Standardabweichung oberhalb des Mittelwerts und ist und bleibt zum Beispiel bei einer normalverteilten Variablen höher als 84,2% aller Werte dieser Variablen, egal welche Skalierung der formalen Beschreibung zugrundeliegt.
2. Multiple lineare Regression
Vorhersage auf der Basis mehrerer Prädiktoren
Sinn der multiplen Regression ist es, die Abhängigkeit einer Variablen von einer Kombination mehrerer anderen Variablen zu untersuchen.
Wir führen unser Beispiel weiter: Die Schulleitung versucht, die Bestimmung der Abiturleistung durch das Heranziehen weiterer Variablen zu verbessern und beauftragt einen Psychologen, die IQs und die Einstellung zur Schule zu messen.
Vorbereitende Übung:
Über Analysieren + Korrelation + Bivariat... erzeugen Sie folgendes Fenster (Abb. 2.1):
Abb. 2.1 SPSS-Steuerungsfenster für bivariate Korrelationen
Mit Einfügen (nicht mit OK!) erzeugen Sie einen Syntaxbefehl und ergänzen Sie ihn wie folgt um das Wort with (nicht nötig, aber es reduziert die Anzahl Koeffizienten auf das Notwendige):
CORRELATIONS
/VARIABLES= attitude chancen IQ with leistung
/PRINT=TWOTAIL NOSIG
/MISSING=PAIRWISE .
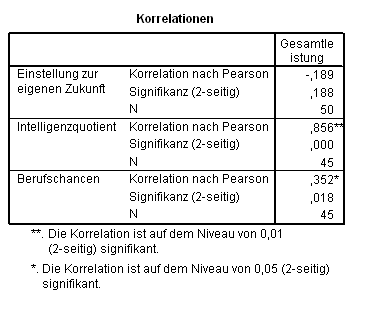
Führen Sie diesen Befehl aus. Das Ergebnis (Tab. 2.1) zeigt die Korrelationen der Variablen leistung mit den Variablen attitude, IQ, und chancen:
Tab. 2.1 Mit with gestaltete Korrelationsmatrix
Über Grafiken + Streudiagramm... und die Option Matrix sowie den Grafikeditor erzeugen Sie folgende Grafik (Abb. 2.2) der Interkorrelationen zwischen dern Variablen attitude, IQ, chancen und leistung:
Abb 2.2 Streudiagramm für mehrere Variablen
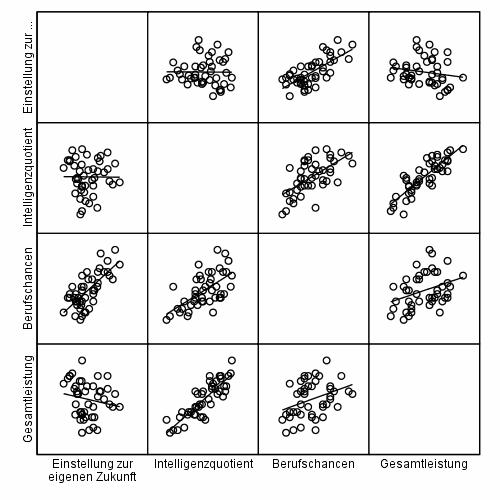
Diese Grafik enthält Streudiagramme für alle Paare der dargestellten Variablen. Die hohe Korrelation zwischen Leistung und IQ und die niedrigere zwischen der Leistung und den Berufschancen, so wie die Unabhängigekt der Variablen IQ und attitude sind deutlich zu sehen. Auch die Streuungen der Variablen um die jeweilige Regressionslinie enthalten interessante Informationen. So kann zum Beispiel die Abiturleistung ziemlich präzise vom Intelligenzquotienten bestimmt werden.
Von besonderem Interesse sind die Korrelationskoffizienten mit der Variablen leistung: IQ (r = 0,856, p < 0,001), chancen (r = 0,352, p < 0,05). Da die Einstellung zur Schule (attitude) kaum mit der Schulleistung korreliert (r = -0,177, p = 0,246, n.s.), könnten wir schon jetzt überlegen, ob wirauf diese Variable verzichten. (Allerdings gibt es Anwendungen, wo genau solche Variablen, die mit den Prädiktoren und nicht mit der abhängigen Variablen, von Interesse sein können. Diese werden später unter dem Begriff "Suppressoren" erklärt.)
Wir suchen eine lineare Kombination der unabhängigen Variablen chancen und IQ, die im Sinne des Mindestquadratkriteriums die Leistung der Schüler am besten vorhersagt ? das heißt: Wir untersuchen die Abhängigkeit der Leistung von chancen und IQ gleichzeitig.
Die Steuerung der Prozedur läuft wie bei der einfachen Regression über Analysieren + Regression + Linear.... (Abb. 2.3):
Abb. 2 3 SPSS-Steuerungsfenster für Multiple Lineare Regression
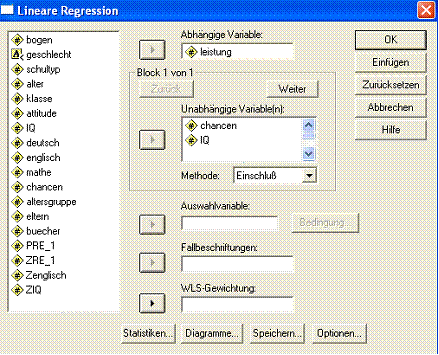
Hier wird die Variable leistung in Abhängigkeit von den Variablen chancen und IQ untersucht.
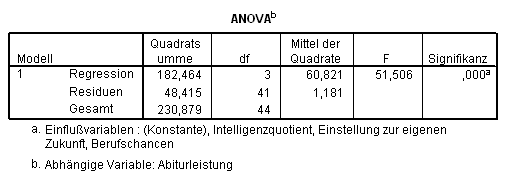
Das Modell (Tab. 2.2) ist eine deutliche Verbesserung gegenüber der einfachen Variante:
Tab. 2.2 Verbesserte Erklärung der Varianz durch Hinzufügen weiterer Prädiktoren

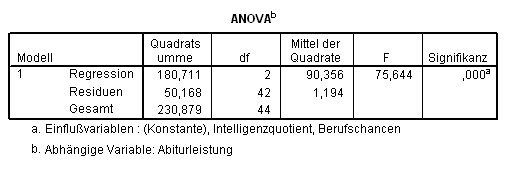
Rund 77% (korrigiertes R-Quadrat) der Varianz der Variablen Leistung kann durch die Variablen chancen und IQ zusammen erklärt werden. Dieser durch die Regression erklärte Varianzanteil ist auch im Vergleich zur Gesamtvarianz hochsignifikant (F = 75,664, d.f. = 2, p < 0,001).
Die Koeffizienten (Tab. 2.3)
Tab. 2.3 Koeffizienten einer multiplen linearen Regression
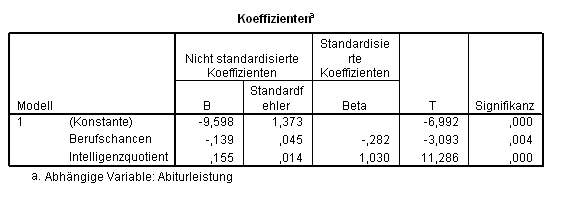
liefern die Gleichung:
leistung = 0,155 × iq ? 0,139 × chancen ? 9,598. (Gl. 2.1)
Die für diese Gleichung benutzten B-Koeffizienten dienen dazu, die individuell beobachteten Rohwerte der Variablen IQ und chancen so zu gewichten, dass die optimale Schätzung der Leistung berechnet wird. Da aber diese Variablen in völlig unterschiedlichen Messeinheiten gemessen wurden, können die B-Koeffizienten nicht unmittelbar miteinander verglichen werden: Der IQ hat einen theoretischen Mittelwert von 100, Standardabweichung 15; der Bogen zur Quantifizierung der Berufschancen einen theoretischen Mittelwert von 10, Standardabweichung 5. Man könnte natürlich beide Variablen vorher standardisieren, so dass beide mit gleichem Mittelwert (typischerweise: 0) und gleicher Standardabweichung (typischerweise: 1) vergleichbar würden, um dann die Regression zu wiederholen und vergleichbare Koeffizienten zu erhalten.
Dieser Vorgang ist aber nicht nötig, denn die Beta-Koeffizienten sind genau diese standardisierten Koeffizienten: Der absolute Wert dieser Beta-Koeffizienten kann demnach als relative Wichtigkeit der enstprechenden Variablen für die Vorhersage interpretiert werden: Der IQ trägt also 1,030 / 0,282, das heißt: über dreeinhalb Mal mehr als die Berufschancen zur Vorhersage der Leistung bei. Auch die T-Werte sind ein Versuch, die Wichtigkeit der unabhängigen Variablen zu quantifizieren: SPSS berechnet diese Werte als B-Koeffizient durch dessen Standardfehler geteilt. Als Hinweis dafür, welche Variablen für die Vorhersage brauchbar sind, wird oft das ziemlich grobe Kriterium benutzt: T-Werte deutlich kleiner -2 oder größer +2 sind akzeptabel. Nach diesem Kriterium tragen sowohl die Berufschancen (T = -3,093) als auch der IQ (T = 11,286) zur Vorhersage bei. (Vorsicht: Die mit den T-Werten verbundenen p-Werte dürfen nicht als Maß der relativen Wichtigkeit der Variablen interpretiert werden, da diese nur für einzelne Variablen relevant sind!)
Wie werden die Variablen in der Gleichung aufgenommen?
Das Einschluss-Verfahren
Falls man genau weiß, welche Variablen in der Regressionsgleichung aufgenommen werden müssen, so benutze man die voreingestellte Methode Einschluss: Alle angegebenen Variablen werden für die Vorhersage benutzt.
Über Analysieren + Regression + Linear und folgendes Steuerfenster (Abb. 2.3) führen Sie die Analyse durch:
Abb. 2.4 Ausgefülltes SPSS-Steuerungsfenster für Multiple Lineare Regression
Unsere frühere Korrelationsanalyse hat schon gezeigt, dass von der Variablen attitude ("Einstellung zur Schule") nicht viel zu erwarten ist. Die Einschluss-Methode zwingt sie trotzdem in die Gleichung (Tab. 2.4):
Tab. 2.4 Zusammenfassende statistiken zur Multiplen Linearen Regression

Diese Gleichung ist minimal besser als unsere erste Variante (R2 hier 0,790; bei dem ersten Modell 0,783); jedoch trägt attitude nicht annähernd signifikant zur Vorhersagekraft der Gleichung bei (Tab. 2.5):
Tab. 2.5 Ergebnisparameter der angepassten multiplen linearen Regression
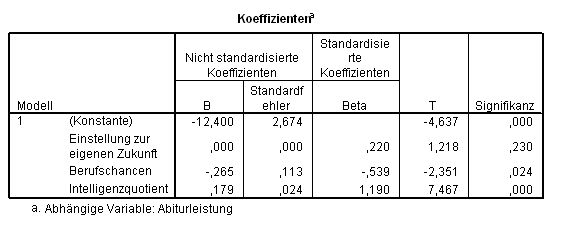
Die Einschluss-Methode ist besonders dann angebracht, wenn die unabhängigen Variablen untereinander unkorreliert sind.
Um dies zu verdeutlichen, vergleichen Sie die gerade erzeugten Beta-Gewichte (Tabelle 2.5) für IQ und chancen (Einstellung zur eigenen Zukunft) mit denen der vorherigen Analyse (Tabelle 2.3). Die Koeffizienten für IQ und chancen haben sich deutlich verändert, weil eine zusätzliche Variable in der Gleichung aufgenommen wurde, die mit IQ und chancen korreliert. Erkärung: Die Beta-Gewichte betreffen den Anteil eines Prädiktors, der nicht mit den restlichen korreliert ? d.h. die Beta-Gewichte betreffen den von den anderen Prädiktoren linear unabhängigen Teil des Prädiktors. Dies könnte die inhaltliche Interpretation erschweren: Denn was ist der Anteil von IQ, der nicht mit der Einstellung zur eigenen Zukunft und nicht mit den erwarteten Berufschancen korreliert?
Das Schrittweise-Verfahren
Sind, wie im aktuellen Beispiel (und im typischen Anwendungsfall), die Prädiktorvariablen untereinander doch korreliert, so wird gewöhnlich das Schrittweise-Verfahren angewendet. Kehren wir zu unserem ursprünglichen Beispiel zurück: Die abhängige (Ziel-)Variable ist leistung, die Prädiktoren attitude, chancen und IQ.
Beim schrittweisen Verfahren wird zunächst die mit der abhängigen Variablen am höchsten (positiven oder negativen) korrelierenden Variablen in der Gleichung aufgenommen ? in unserem Fall also IQ. Die partiellen Korrelationen der restlichen Variablen mit der abhängigen Variablen, "bereinigt" also von der schon aufgenommenen Variablen, werden berechnet, und die Variable mit der höchsten (positiven oder negativen) partiellen Korrelation in der Gleichung aufgenommen. Diese partiellen Korrelationen versteht man am besten anhand eines Beispiels:
Über Analysieren + Korrelation + Partiell. . . erzeugen Sie folgendes (hier schon ausgefülltes) Fenster (Abb. 2.5):
Abb. 2.5 SPSS-Steuerfenster zur partiellen Korrelation
Bei diesen partiellen Korrelationen werden die Auswirkungen der Variablen IQ "beseitigt": Das heißt, lediglich die Anteile der anderen Variablen, die nicht mit IQ korrelieren, werden für partielle Korrelationskoeffizienten benutzt, die Anteile also, die (linear) "nichts mit IQ zu tun haben".
Das Ergebnis (2.6):
Tab. 2.6 Ergebnis einer Partiellen Korrelationsanalyse
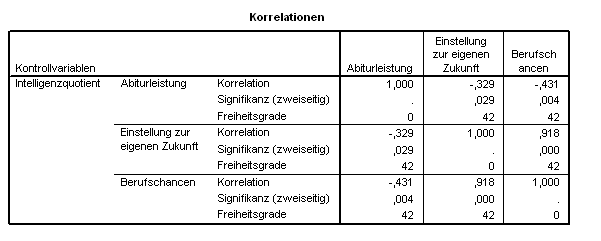
Zunächst sollte diese Matrix inhaltlich untersucht werden: Entfernt man aus attitude und chancen der Anteil, der durch den IQ bestimmt wird, so korrelieren diese "bereinigten" Variablen nun negativ mit leistung: Der bisherige, stark positive Zusammenhang zwischen leistung (bzw. attitude) und chancen kann teilweise durch den IQ erklärt werden. Man könnte demnach in Erwägung ziehen, IQ als alleinigen Vorhersager der Abiturleistung heranzuziehen (was sowohl intuitiv als auch theoretisch Sinn machen würde).
Fahren wir aber mit dem Regressionsvorgang fort: Die höchst korrelierende Prädiktorvariable IQ ist schon in der Gleichung eingebaut. Die (absolut) höchste partielle Korrelation der unabhängigen Variablen mit leistung, nachdem die Effekte von IQ entfernt wurden, ist nun die mit chancen, die als zweiter Schritt in der Gleichung aufgenommen wird.
Dieses Auswahlverfahren wird fortgesetzt, jedoch wird bei jedem Schritt überprüft, ob schon aufgenommene Variablen aus der Gleichung entfernt werden können, ohne die Vorhersagekraft signifikant zu verringern (durchaus möglich, denn Variablenkombinationen können andere Variablen redundant machen).
Dies geschieht über den F-Wert. Wiederholen Sie die letzte Regressionsanalyse, wählen Sie jedoch die Methode Schrittweise aus (Abb. 2.6):
Abb. 2.6 Steuerung der schrittweisen multiplen linearen Regression
Nebenbei inspizieren Sie das über Optionen... erreichbare Fenster (Abb. 2.7):
Abb 2.7 Optionen bei der SPSS-Steuerung der multiplen linearen Regressionsanalyse
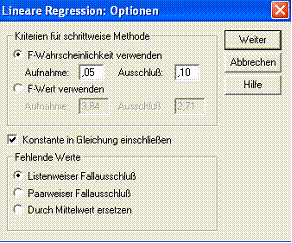
Unter Kriterien für schrittweise Methode können Sie die F-Werte bzw. die entsprechenden Wahrscheinlichkeitswerte für das schrittweise Verfahren bestimmen. Voreingestellt werden die mit dem F-Wert verbunden p-Werte zum Verfahren herangezogen: Eine Variable wird in der Gleichung erst dann aufgenommen, wenn der entsprechende F-Wert einen Signifikanzniveau von p < 0,05 erreicht. Bei jedem Schritt des Verfahrens wird auch untersucht, ob Variablen entfernt werden können: Falls der Signifikanzniveau für eine Variable p < 0,10 nicht (mehr) erreicht, so wird diese aus der Gleichung entfernt. Ohne diese Voreinstellung zu ändern (das heißt: Schließen Sie das Fenster mittels Abbrechen!), führen Sie die Analyse aus (Tab 2.7)!
Tab. 2.7 Protokoll des Ablaufs einer schrittweisen multiplen Regression

Das Stepwise-Verfahren hat zwei Modelle (Tab. 2.7) durchgeführt:
- Beim ersten Schritt (Modell 1) wurde der IQ in der Gleichung aufgenommen.
- Beim zweiten Schritt (Modell 2) wurde die Variable chancen (Berufschancen) hinzugefügt und keine Variable entfernt, so dass das 2. Modell zwei unabhängige Variablen enthält.
Was ist mit unserer dritten Variablen attitude passiert? Die Antwort enthält die letzte Ausgabetabelle (Tab. 2.8), die aus der Gleichung ausgeschlossene Variablen (Ausgeschlossene Variablen) dokumentiert:
Tab. 2.8 Protokoll der aus der Regression ausgeschlossenen Variablen
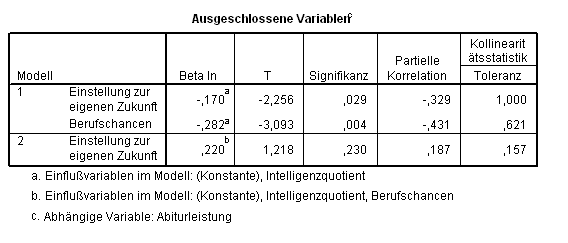
Beim ersten Schritt (Modell 1) wurden weder attitude noch chancen in der Gleichung aufgenommen. Beim zweiten Schritt (Modell 2) wurde chancen hinzugefügt. Das logisch mögliche dritte Modell wird gar nicht berechnet, da die Variable attitude das Kriterium zur Aufnahme in der Gleichung nicht erfüllt (die Signifikanz von 0,230 ist deutlich höher als das vorgegebene Signifikanzniveau von 0,05).
Das Problem der korrelierten Prädiktoren
Der Vergleich der Beta-Koeffizienten, um die relative Wichtigkeit von Prädiktoren zu bestimmen, birgt bei korrelierten Prädiktoren eine große Gefahr, die wir am besten anhand eines Beispiels erklären.
Die Schulleitung interessiert die Hintergründe der Abiturleistung. Sie wenden zwei weitere Testbögen an, die 1. das Interesse der Eltern für die Leistung ihrer Kinder und 2. die Anzahl Bücher im Haushalt messen.
Berechnen Sie mit der Stepwise-Methode die Regression der Variablen IQ, eltern und buecher auf leistung (Tab. 2.9)!
Tab. 2.9 Zusammenfassung eines angepassten multiplen linearen Rgressionsmodells

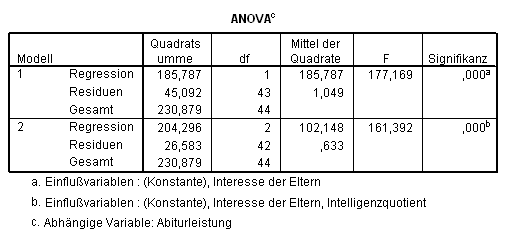
Zwei Modelle sind mit den Prädiktoren berechnet worden: Interesse der Eltern (Modell 1); und Interesse der Eltern zusammen mit dem IQ (Modell 2). Beide Modelle scheinen akzeptabel zu sein. Die Anzahl Bücher im Haushalt wird als Prädiktor vom Verfahren nicht eingesetzt, da diese Variable nicht signifikant mehr zur bestehenden Gleichung beiträgt.
Versuche man nun die Beta-Koeffizienten (Tab. 2.10) zu interpretieren:
Tab. 2.10 Ausgabe der multiplen linearen Regression ? vorsicht bei korrelierten Prädiktoren!
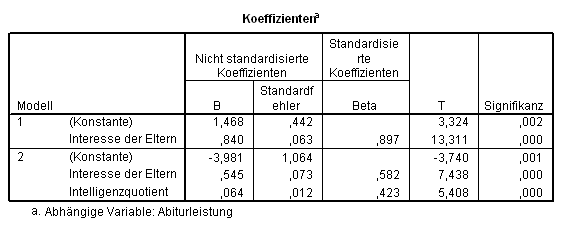
so könnte man dazu verleitet werden, den Schluss zu ziehen, die Schulleistung hänge mehr vom Interesse der Eltern ab als vom IQ (diese Interpretation unserer Ergebnisse wäre korrekt) und, dass die Anzahl Bücher im Haushalt überhaupt keine Aussagekraft besitzt ? und diese Interpretation wäre gänzlich falsch. Die Tabelle zu den ausgeschlossenen Variablen (Tab. 2.11) enthält Hinweise hierzu:
Tab. 2.11 Statistiken zu den aus dem Regressionsmodell ausgeschlossenen Variablen
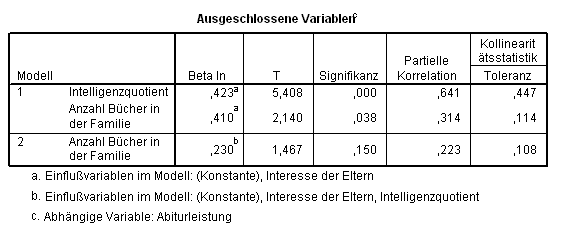
Die Kollinearitätsstatistik ist speziell dann relevant, wenn Prädiktoren untereinander korrelieren. Der hier besonders wichtige Toleranzwert wird als
Toleranz = 1 ? Ri2 , (Gl. 2.2)
wobei Ri2 die quadrierte multiple Korrelation der i-ten Variablen mit den anderen Prädiktoren ist. Die Toleranz beschreibt also die Proportion der Prädiktor-Varianz, die durch die i-te Variable erklärt werden kann. Für IQ ist dieser Toleranzwert bei Modell 1 zum Beispiel 0,447. Kleinere Toleranzwerte für eine bestimmte Variablen sind ein Indiz dafür, dass die restlichen Prädiktoren schon so viel Varianz erklären, dass diese Variable keinen zusätzlich signifikanten Beitrag zur Gleichung bringen kann. Es impliziert also auch, dass diese Variable zum Teil als lineare Funktion der restlichen Variablen beschrieben werden kann. Und das wiederum heißt, dass die Schätzung des Regressionskoeffizienten für diese Variablen instabil und völlig unbrauchbar ist.
Den Schluß zu ziehen, die Anzahl Bücher im Haushalt hätte nichts mit der Schulleistung zu tun, wäre völlig falsch: Berechnen Sie die einfache Regression von buecher auf leistung, so sehen Sie, dass die Anzahl Bücher im Haushalt durchaus ein wichtiger Prädiktor der Schulleistung ist: Die Variable buecher verschwindet aus der multiplen Regression lediglich dadurch, dass sie mit anderen Prädiktoren so hoch korreliert, dass sie kaum zusätzliche Information (Varianzerklärung) zur Gleichung beitragen kann.
Übung:
Berechnen Sie die Korrelationskoeffizienten zwischen den Variablen leistung, buecher, iq, eltern!
Alle drei Prädiktoren korrelieren hoch mit der vorherzusagenden Variablen. Alle drei könnten demnach eine gute Vorhersage liefern. Sie korrelieren aber auch untereinander so hoch, dass, ist eine Variable schon Teil der Gleichung, die anderen lediglich nur noch relativ wenig zusätzliche Information liefern können.
Berechnen Sie die partielle Korrelation von buecher mit leistung, korrigiert für iq und eltern (Tab. 2.12):
Tab. 2.12 Partielle Korrelation: Ausgabe

Es bleibt nur noch (0,223)2 = weniger als 5% Gemeinsamkeit zwischen den beiden übrigen Variablen. Kein Wunder, also, dass die Gleichung keinen Platz für buecher findet ? trotz der Tatsache, dass diese Variable ein hervorragender Prädiktor der Schulleistung wäre!
Was tun bei korrelierten Prädiktoren?
Da korrelierte Prädiktoren, wie gerade gesehen, in der Regel zu schwer interpretierbaren Regressions-Ergebnissen führen, stellt sich die Frage, ob man das Regressionsmodell bei korrelierten Daten trotzdem anwenden kann.
Die klassische Lösung zu diesem Problem besteht darin, die Daten so zu transformieren, dass sie nicht mehr korreliert sind. Dies geschieht häufig über die Hauptkomponentenanalyse, die lineare Kombinationen der Variablen, sogenannte "Komponenten" (manchmal nicht ganz korrekt auch "Faktoren" genannt) sucht, die untereinander nicht korreliert und somit für das Regressionsmodell unproblematisch sind. Die Hauptkomponentenanalyse wird an dieser Stelle nicht weiter diskutiert: Konsultieren Sie dazu einen kompetenten Fachberater.
Suppressor-Variablen
Genau diese Tatsache, dass nur der Anteil eines Prädiktors zur Gleichung beitragen kann, der unabhängig ist von anderen Prädiktoren, kann man sich zunuzte machen, um die Auswirkungen von Störvariablen zu beseitigen. Eine besonders gefährliche Art von Störvariablen ist der so genannte "Suppressor", eine Variable, die gerade nicht mit der Zielvariablen, aber doch mit den anderen Prädiktoren korreliert. Die Gefahr des Suppressors liegt gerade darin, dass er nicht mit der Zielvariablen korreliert und daher fälschlicherweise als irrelevant eingestuft werden könnte.
Als Beispiel nehmen wir an, wir möchten die Einstellung zur Schule (attitude) anhand der Variablen "Berufschancen" (chancen) und der Abiturnote (leistung) schätzen. Allerdings möchten wir diese Gleichung "bereinigt" von den Auswirkungen des IQ.
Folgende Korrelationsmatrix (Tab. 2.13) zeigt, dass der IQ als Suppressor-Variablen betrachtet werden kann, denn sie korreliert mit den beiden Prädiktoren chancen und leistung, aber nicht mit der Ziel-Variablen attitude:
Tab. 2.13: Korrelationen aller Prädiktoren unter sich und mit der Zielvariablen

Wir benutzen also die Einschluss-Methode, um auch diese Variablen in die Gleichung zu zwingen (Abb. 2.8):
Abb. 2.8 Steuerung eines Modells mit Suppressor-Variablen
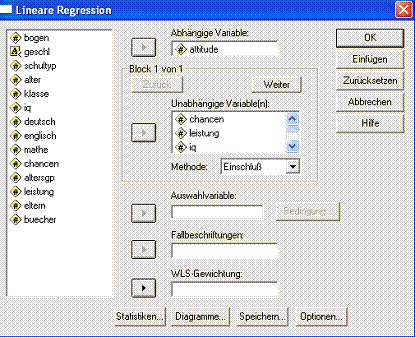
Das Ergebnis (Tab. 2.14):
Tab. 2.14 Ergebnis einer Analyse mit Suppressor-Variablen
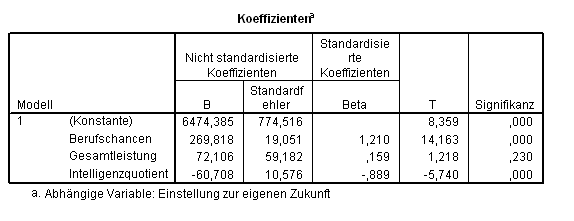
Sowohl der Beta-Koeffizient zur Variablen IQ als der mit dem T-Test verbundene Signifikanzwert bestätigen, dass der Anteil dieser Variablen, der nicht mit den anderen Prädiktoren korreliert, kräftig zu der Vorhersage beiträgt. Allerdings betrachten wir diese Variable inhaltlich als Störvariablen, deren Auswirkungen wir beseitigen möchten - und genau das haben wir mit unserer Analyse bewirkt, denn die B- und Beta-Werte der beiden inhaltlich interessanten Prädiktoren chancen und leistung sind genau die gewünschten: die, die vom Einfluss der Suppressor-Variablen bereinigt sind. Nach Beseitigung der Auswirkungen vom IQ, also, trägt die Schätzung der Berufschancen deutlich über 11 mal mehr zur Bestimmung der Einstellung zur Zukunft als die Abiturleistung.
Hätten wir diese Suppressorvariablen einfach ignoriert, so sähen die B- und Beta-Koeffizienten und daher unsere Interpretation ganz anders aus (Tab. 2.15):
Tab. 2.15 Koeffizienten einer Analyse mit Suppressor-Variablen
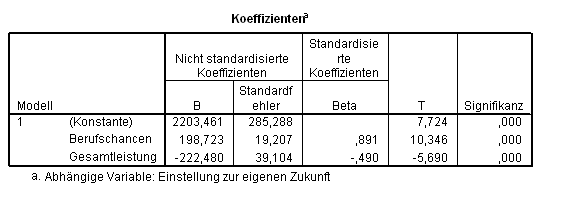
Hier, ohne Beseitigung des Einflusses der Suppressor-Variablen, würde man die Berufschancen als rund doppelt so wichtig in der Vorhersage von der Einstellung zur eigenen Zukunft als die Abiturleistung ? die auch noch negativ zur Vorhersage beiträgt: Je niedriger die Leistung, desto positiver die Einschätzung der eigenen Zukunft. Genau die gegenteilige Interpretation resultiere von der Analyse mit unserer Suppressor-Variablen.
Ein sicherer Anpassungsvorgang
Bisher haben wir unser Regressionsmodell anhand der Daten aller verfügbaren Kinder angepasst und gewisse Kriterien der Güte des Modells und der Anpassung verlangt. Das heißt: Wir haben ein für unsere Stichprobe optimales lineares Regressionsmodell entwickelt. Es ist ? wie oben kurz angesprochen ? kaum zu erwarten, dass dieses Modell bei anderen Stichproben auch optimal sein könnte.
Genau das aber verlangt die Praxis: Wir wollen anhand von gemessenen Variablen die Werte einer nicht gemessenen (oft sogar aus praktischen Gründen nicht mehr messbaren) Variablen schätzen. In unserem Beispiel versuchen wir, bei Elfjährigen die zu erwartende Abiturleistung vorherzusagen. Mediziner versuchen etwa anhand von gemessenen Werten (Lungenfunktion, Blutwerten ...) den Grad einer Erkrankung zu bestimmen. Das typische Regressionsmodell passt aber selbstverständlich besser bei der Gruppe, die zur Bestimmung der Gleichung herangezogen wird, als bei der Zielgruppe (neue Schüler, Patienten, ...). Diese Gefahr ist besonders hoch bei Regressionsmodellen mit vielen unabhängigen Variablen: Je mehr Variablen, desto größer die Gefahr, dass das Modell bei einer zweiten Stichprobe sogar völlig falsch liegen kann.
Was tun? Zunächst sollte man stets die korrigierten R2-Werte als Bestimmtheitsmaß nehmen, denn diese korrigieren genau dafür, dass ein Modell bei einer neuen Stichprobe angewendet wird. Aber auch diese Korrektur reicht für viele Forscher nicht aus: Ein sicherer Vorgang besteht darin, die Gleichung bei einer zufällig ausgewählten Untermenge der Stichprobe zu bestimmen, um sie anschließend bei den restlichen Probanden zu testen. Dieser Ansatz nennt sich Kreuzvalidierung.
Vier Schritte sind dazu notwendig:
- eine Zufallsauswahl eines bestimmten Prozentsatzes der Gesamtstichprobe wird selektiert: Häufige Werte hierfür sind 60%, 70% oder 80% der Gesamtstichprobe.
- Das Regressionsmodell wird bei dieser Teilstichprobe angepasst und die Gleichung bestimmt.
- Anhand der Koeffizienten der Regressionsgleichung werden die geschätzten Werte der abhängigen Variablen für die restlichen Probanden berechnet.
- Der Korrelationskoeffizient zum Quadrat (r2) zwischen den tatsächlich beobachteten und den geschätzten Werten wird auf der Basis der zweiten Stichprobe berechnet und als Bestimmtheitsmaß herangezogen.
Wir führen dies für unsere Stichprobe durch:
Über Daten + Fälle auswählen wählen und der abhängigen Variablen leistung, Prädiktoren IQ und chancen. Bei der Auswahl für die vorliegende Schrift wurden auf dieser Weise folgende Koeffizienten (Tab. 2.16) errechnet:
Tab. 2.16 Koeffizienten der Gleichung bei einer Unterstichprobe

Merken Sie nebenbei, dass diese Gleichung sich klar von der unterscheidet, die wir auf der Basis der Gesamtstichprobe erhalten haben (Gl. 2.1)! Das Regressionsmodell ist eben nicht stabil.
Beim Selektionsvorgang generiert SPSS automatisch die Variable filter_$: Diese enthält den Wert 1 für die selektierten Fälle, 0 für die ausgeschlossene. Über Daten + Fälle auswählen. . ., Falls Bedingung zutrifft und den Knopf Falls selektieren Sie nun genau die Fälle, die vorher nicht selektiert waren, die also, die filter_$ = 0 aufweisen. (Dadurch ändert sich natürlich auch der Wert der Variablen filter_$: 1 wird zu 0, 0 zu 1.)
Mittels Transformieren + Berechnen. . . berechnen Sie die auf der Basis dieser Regressionskoeffizienten die geschätzte Leistung, in unserem Falle also:
ges_leis = 0,164 × iq - 0,l75× chancen - 10,244 . (Gl. 2.3)
Die Frage nun ist: Wie hoch korrelieren diese geschätzten Werte mit den tatsächlich beobachteten Werten?
Über Analysieren + Korrelation + Bivariat. . . berechnen Sie den Korrelationskoeffizienten zwischen leistung und ges_leis und quadrieren Sie diesen Koeffizienten: Dadurch erhalten Sie eine Schätzung von r2. Der Wert 100 × (1 - r2) gibt als Prozent den Anteil der Varianz wieder, der durch die Gleichung nicht erklärt werden kann.
Mit Glück werden Sie mit diesem Datensatz ca. 75% der Varianz erklären können ? ein ernüchternd kleiner Wert. Salopp ausgedrückt: Solche Schätzungen (und damit die Regressionsgleichung) liegen ca. 25% falsch. Ein Grund für diesen niedrigen Wert ist der, dass unsere kleinere Stichprobe wirklich zu klein ist, um den Koeffizienten gut zu bestimmen. Dies führt zur Frage: Wie groß soll die Stichprobe für die Bestimmung einer Regressionsgleichung sein?
Stichprobengröße
Im Prinzip ist die Antwort auf die Frage: Wieviele Probanden braucht eine Regression? ? ,,so viele wie möglich?. Aber dazu eine wichtige Warnung: Verlassen Sie sich niemals nur auf die Signifikanzwerte! Denn diese sind auch durch die Stichprobengröße bestimmt: Siehe die Diskussion in [2] zum Thema "Signifikanz und Relevanz". Bei einer großen Stichprobe kann ein Modell hochsignifikant sein, obwohl die Regressionsgerade fast parallel zur X-Achse liegt, so dass für die Praxis brauchbare Koeffizienten kaum bestimmt werden konnten. Empfehlung: Wenden Sie immer das Kreuzvalidierungsverfahren an! Das so bestimmte R2 ist eine vertretbare Quantifizierung der Güte des Modells.
3. Binäre logistische Regression
Vorhersage auch anhand kategorieller Variablen
Anstelle von einfachen Gewichtungen der Prädiktoren, basiert die logistische Regression auf Schätzungen der Wahrscheinlichkeit eines Ereignisses. Der große Vorteil dieses Modells ist seine Fähigkeit, auch kategorielle Variablen sowohl als abhängige (Ziel-) als auch als unabhängige Variablen (Prädiktoren) in Betracht zu ziehen. Zum Beispiel: Wie hoch ist die Wahrscheinlichkeit eines Herzinfarkts abhängig von der Anzahl täglich gerauchter Zigaretten, des Alters und des Geschlechts des Patienten? Die abhängige Variable hier ist dichotom: Herzinfarkt ja (1) oder nein (0).
Die Basisgleichung einer einfachen binären logistischen Regression ähnelt der der einfachen linearen Regression:
Z = C + BX , (Gl. 3.1)
und die Wahrscheinlichkeit, dass das Ereignis Z beobachtet wird (die Wahrscheinlichkeit, in unserem Beispiel, dass ein Herzinfarkt eintreten wird) wird anhand einer logistischen Funktion definiert:
Pr (Ereignis) = 1 / (1 + e-Z) , (Gl. 3.2)
wobei Pr (Englisch: Probability) "Wahrscheinlichkeit" bedeutet.
Ein Beispiel verdeutlicht: Als abhängige Variablen nehmen wir Geschlecht, kodiert 0 = männlich, 1 = weiblich. Wir wollen untersuchen, inwieweit das Geschlecht unserer Schüler anhand der Variablen chancen vorhergesagt werden kann, die die geschätzten Chancen von beruflichem Erfolg widergibt. In diesem Fall: Wie hoch ist die Wahrscheinlichkeit, eine Schülerin (geschl = 1) zu sein, in Abhängigkeit von der Variablen beruf?
Über Analysieren + Regression + Binär logistisch... erhält man folgendes Steuerfenster (Abb. 3.1), hier mit den Variablen schon in ihre Felder übertragen:
Abb. 3.1 SPSS-Steuerungsfenster zur binär-logistischen Regression
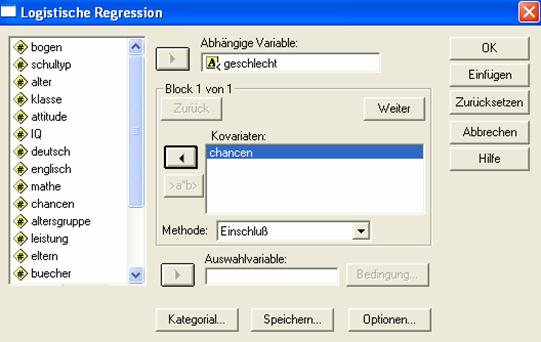
Das Programm passt die Gleichung an und schätzt (Tab. 3.1) anhand dieses angepassten Modells die Geschlechtszugehörigkeit von jedem Fall. Folgende Tabelle vergleicht die daraus resultierende Zuordnung (männlich oder weiblich) auf der Basis der Variablen chancen mit der tatsächlichen Geschlechtszugehörigkeit:
Tab. 3.1 Güte des Modells anhand einer Klassifizierungstabelle
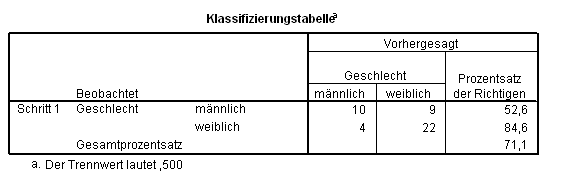
angenommen, es wäre unser Ziel, das Geschlecht "männlich" anhand unserer Prädiktoren "vorherzusagen", könnten wir die traditionellen Statistiken berichten:
Sensitivität: 10 / (10+22) = 0,31
Spezifizität: 9 / (9+22) = 0,29
positiver Wahrscheinlichkeitswert: 10 / (10+4) = 0,71
negativer Wahrscheinlichkeitswert: 22 / (9+22) = 0,71.
Das Geschlecht von 10 aus 19 (52,6%) Schülern, 22 aus 28 (84,6%) Schülerinnen, insgesamt 77,1% aller Schüler unserer Stichprobe wird korrekt vorhergesagt. Aber: Im Falle der (männlichen) Schüler ist dieser Trefferquote nicht annähernd akzeptabel ? das Modell klassifiziert fast die Hälfte aller Jungen als Mädchen!. Auch die geschätzten R2-Werte der Modellzusammenfassung sind unbefriedigend: Die Snell & Cox-Schätzung liegt bei 0,117: Weniger als 12% der Variation der Variablen geschl kann durch die Variablen chancen erklärt werden.
Das Modell selbst (die angepasste Gleichung) wird in folgender Tabelle (Tab. 3.2) dargestellt:
Tab. 3.2 Parameter des angepassten logistischen Regressionsmodells

Betrachten wir zunächst den Regressionskoeffizienten B, hier mit dem geschätzten Wert -0,165. Die geschätzte Wahrscheinlichkeit des Ergeignisses geschl = 1 (d.h., dass eine Person weiblich ist) ist:
Pr(weiblich) = 1 / (1 + e-Z) , (Gl. 3.3)
wobei
Z = 1,994 ? 0,165 × chancen . (G. 3.4)
Betrachten wir nun einen spezifischen Fall mit dem beobachteten Wert chancen = 10:
Z = 1,994 ? 1,65 = 0,344 (Gl. 3.5)
sodass
Pr (weiblich) = 1 / (1 + e?0,344) = 0,585 . (Gl. 3.6)
und daher
Pr (nicht weiblich) = 1 ? Pr(weiblich) = Pr(männlich) = 0,415 . (Gl. 3.7)
Falls wir nun eine Wette abschließen würden, dass eine Person mit dem Wert chancen = 10 eine Frau ist, so wären unsere Chancen zu gewinnen (der englische Begriff, auch im deutschen in diesem Kontext benutzt, heißt odds)
Odds(weiblich) = Pr(weiblich) / Pr(nicht weiblich) = 0,585 / 0,415 = 1,410 . (Gl. 3.8)
Ein Odds von 1 spiegelt gleiche Chancen wider, sodass unsere Chancen, unsere Wette zu gewinnen, leicht besser sind, wenn wir weiblich als wenn wir männlich tippen würden.
Im Kontext der logistischen Regression wird meist der Logarithums der Odds, "log odds" benutzt:
ln[Odds(weiblich)] = ln(1,410) = 0,344. (Gl. 3.9)
Ein log odds von 0 bedeutet gleiche Chancen für das Ereignis (hier: weiblich) wie für das nicht-Ereignis (hier: nicht-weiblich = männlich).
Übungen
Das Trinkverhalten einer Stichprobe von Patienten wurde untersucht, die alle behaupten, mit Alkohol ihr empfundenes Stresslevel reduzieren zu können. Öffnen Sie die Datei alcohol.sav! Inspizieren Sie die Variablendefinition, um den Inhalt des Datensatzes zu verstehen!
Fassen Sie die Daten deskriptiv und grafisch zusammen!
Generieren Sie ein Regressionsmodell, das die Abhängigket von Stress nach Alkoholkonsum als lineare Funktion von Stress vor Alkoholkonsum und Alkoholkonsum beschreibt! Interpretieren Sie die Ergebnisse dieser Analyse!
Wiederholen Sie die Analyse, aber für Stadt-/Landbewohner sowie für Männer/Frauen getrennt! Interpretieren Sie auch diese Ergebnisse!
Fassen Sie die gesamten Ergebnisse zusammen und liefern Sie eine gemeinsame Interpretation der Studie!
Literatur
[1] Wiseman, M. (2004) SPSS für Windows: Eine Einführung. München: Leibniz-Rechenzentrum der Bayerischen Akademie der Wissenschaften
[2] Wiseman, M. (2004) SPSS für Windows Special Topics: Einige Grundbegriffe der Statistik. München: Leibniz-Rechenzentrum der Bayerischen Akademie der Wissenschaften