SPSS Special Topics: Einige Grundbegriffe der Statistik

Michael Wiseman

Einführung

Die Schriftreihe Special Topics entstand aus dem Wunsch mehrerer Teilnehmer am LRZ-Einführungskurs SPSS für Windows nach weiteren Informationen, die über die reine Bedienung des Programms hinausgehen. Auch die Themen wurden durch Kunden des LRZ bestimmt, die unsere Spezialisten im Bereich der angewandten Statistik konsultiert haben: Diese Reihe versucht, Informationen zu dort häufig aufkommenden Missverständnissen und Fragen zu geben; sie ist natürlich auf keinen Fall als Ersatz für gute Standardtexte (wie zum Beispiel [1]) zu verstehen.

Die vorliegende Schrift geht davon aus, dass Sie Kenntnisse der Steuerung von SPSS unter Windows besitzen, wie man sie zum Beispiel durch Teilnahme am LRZ-Einführungskurs erwerben kann. Auch die Begleitschrift [2] zu diesem Kurs vermittelt diese Kenntnisse.

Starten Sie SPSS und öffnen Sie die Datei data2.sav!

Skalenniveau

Das Skalenniveau spiegelt die (numerische) Qualität Ihrer Messungen wider.

Nominal

Nominalskalierte Werte haben die Funktion lediglich eines Etiketts und besitzen keine numerische Bedeutung.

Beispiel:

Geschlecht könnte man mit "0" (männlich) und "1" (weiblich) kodieren – aber genauso umgekehrt oder mit "m" und "w" oder "1" und "2" oder …. Da einige SPSS-Prozeduren außerstande sind, Zeichenketten zu verarbeiten, hat es schon einen Sinn, Ziffern zur Kennung solcher Ausprägungen zu benutzen: Aber solche "Zahlen" bleiben – trotz ihres Aussehens – ohne mathematische Bedeutung: "0" etwa bedeutet nicht "besitzt kein Geschlecht"; ebenso wenig bedeutet "2" "hat zweimal soviel Geschlecht wie die Ausprägung 1".

Da nominal skalierte Variablen keine numerische Bedeutung besitzen, hat es auch keinen Sinn, sie mathematisch zu behandeln. Die Datei data2.sav enthält die Variablen geschl, die die Ausprägungen "m" bzw. "w" für "männlich" bzw. "weiblich" aufweist. Die einzigen Fragen, die hier in Frage kämen, sind die, die sich mit den Häufigkeiten (wie viele männliche, wie viele weibliche Probanden) oder mit den relativen Häufigkeiten (z.B.: sind signifikant mehr männliche als weibliche Probanden in der Stichprobe) befassen. Natürlich können solche Variablen zudem als Gruppierungsvariablen (auch – kontextabhängig – "Faktor", "unabhängige Variable" genannt) benutzt werden. Erst in Zusammenhang mit anderen Variablen eines höheren Skalenniveaus werden solche Hypothesen getestet wie: Schülerinnen haben bessere Englischnoten als Schüler.

Ordinalskalierung

Ordinalskalierte Werte besitzen die Eigenschaften einer Nominalskala, geben aber zusätzlich die Rangreihe der Messungen wieder.

Beispiel:

Die Variable altersgp wurde nach folgender Tabelle definiert:

alter	altersgp
bis einschließlich 12 Jahren	1
13 bis einschließlich 15 Jahren	2
16 Jahre und älter	3

Diese Variable enthält die korrekte Rangreihe des Alters: Eine Person der Altersgruppe "1" ist jünger als eine der Altersgruppe "2", die wiederum jünger als eine der Gruppe "3". Man kann aber nicht behaupten, Personen der Altersgruppe "3" wären dreimal so alt wie Personen der Gruppe "1".

Für ordinalskalierte Variablen kommen nichtparametrische Tests in Frage, die speziell u.a. für dieses Skalierungsniveau entwickelt wurden.

Übung:

Benutzen Sie den (nichtparametrischen) Spearman'schen Korrelationskoeffizienten um zu überprüfen, ob Alter und Schulklasse hoch positiv korrelieren (tun sie es nicht, so ist etwas mit unseren Daten nicht in Ordnung)!

Intervallskalierung

Intervallskalierte Werte besitzen die Eigenschaften nominaler und ordinaler Skalen und zusätzlich die, dass der Abstand zwischen den Messwerten aussagekräftig ist.

Beispiel:

Bei Temperatur ist der Unterschied zwischen 100º C und 110º C genauso groß wie der zwischen 1000º C und 1010º C. Dasselbe gilt innerhalb der Fahrenheit-Skala. Der Wert 0º hat jedoch weder bei der Celsius- noch bei der Fahrenheit-Skala den Sinn einer absoluten Nulltemperatur ("überhaupt keine Wärme").

Für die überwiegende Mehrzahl statistischer Verfahren reicht eine Intervallskalierung.

Übung:

Testen Sie mit dem parametrischen Pearson'schen Korrelationskoeffizienten, ob die Mathematiknote positiv mit den Sprachnoten korreliert (sie dürfen davon ausgehen, dass diese Schulnoten normalverteilt sind)!

Verhältnis- (Ratio-, auch Absolut-) Skalierung

Eine Verhältnisskala besitzt alle Eigenschaften der ordinalen, nominalen und Intervall-Skalen und zusätzlich die, dass der Nullpunkt eine Bedeutung hat: Die Kelvin'sche Temperaturskala ist eine solche Skala: "0" heißt dort wirklich "keine Wärme". Weitere Beispiele: Alter (im Gegensatz zu einer Gruppierung von Altersangaben); oder die Anzahl pro Tag gerauchter Zigaretten.

Statistische Verfahren setzen kaum eine Skala dieses Niveaus voraus (können sie aber selbstverständlich problemlos analysieren).

Metrische Skalierung

Das Programm SPSS fasst Intervall- und Verhältnisskalen unter dem gemeinsamen Begriff "metrisch" zusammen.

"Normal" verteilt?

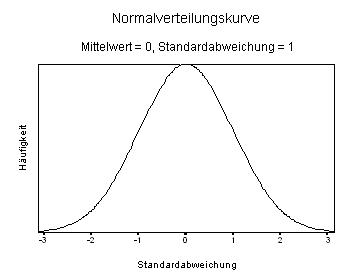
Eine Voraussetzung für die üblichen parametrischen Tests ist die sogenannte "Normalität" der zu untersuchenden Variablen. Die Normalverteilung hat folgende Form:

Die Y-Achse spiegelt die Häufigkeit von Fällen wider. Die meisten Fälle liegen um den Mittelwert (in diesem Beispiel 0). Je weiter vom Mittelwert entfernt, desto weniger Fälle werden beobachtet. Diese Verteilung beschreibt viele in der Natur vorkommende Werte, zum Beispiel die Größe eines Menschen: Die meisten Menschen sind mittlerer Größe, sehr kleine Menschen sind relativ selten (und je kleiner, desto seltener), sehr große Menschen sind relativ selten (je größer, desto seltener).

Die Symmetrie dieser Kurve bedeutet, dass die Hälfte der Werte unter dem Mittelwert (hier: 0) liegen, die Hälfte darüber. Zwischen -1 und +1 Standardabweichungen vom Mittelwert liegen 68% aller Fälle (34% über dem Mittelwert, 34% darunter), zwischen -2 und +2 Standardabweichungen vom Mittelwert befinden sich 96% aller Fälle (48% zwischen dem Mittelwert und +2 Standardabweichung, 48% zwischen dem Mittelwert und -2 Standardabweichung), der Bereich zwischen -3 und +3 Standardabweichungen vom Mittelwert umfasst schon über 99% aller Fälle.

Nehmen wir den berühmt-berüchtigten Intelligenzquotienten (IQ) als Beispiel: Dieser ist per definitionem normalverteilt, mit Mittelwert 100 und Standardabweichung 15. Die Hälfte der (nicht hirngeschädigten) Bevölkerung hat unterdurchschnittliche Intelligenz (IQ-Werte unter 100). Um dagegen einen guten Universitätsabschluss erfolgreich zu erreichen brauche man – so nehmen wir nicht ganz unrealistisch an – einen IQ von 130, das heißt: zwei Standardabweichungen oberhalb des Mittelwerts. Eine Person mit einem IQ von 130 ist demnach intelligenter als (50% + 48% =) 98% der Bevölkerung.

Die wichtigsten und mächtigsten statistischen Tests (die so genannten parametrischen Tests) setzen eine Normalverteilung der zu untersuchenden Variablen voraus: Diese Voraussetzung der Normalität bedeutet aber nicht, dass Ihre Daten in sich ein perfekte Normalverteilung aufweisen, sondern dass Ihre Daten aus einer Normalverteilung in der Gesamtbevölkerung stammen, aus der die Stichprobe per Zufall gezogen wurde. Eine endliche Menge von Messungen kann gar nicht perfekt normalverteilt sein.

Wir können zum Beispiel nicht erwarten, dass die IQ-Werte einer einzigen Schulklasse, oder einer einzigen Schule, oder aller bayerischen Schulen, eine perfekte Normalverteilung aufweisen: Das sind sie nur im Limit, d.h. mit einer unendlich großen Stichprobe. ebenso wenig können wir erwarten, dass unser kleiner Datensatz perfekt normalverteilte IQ-Werte aufweist, trotz der Tatsache, dass diese aus einer mathematischen Normalverteilung generiert wurden.

Übung:

Erzeugen Sie über Grafiken + Histogramm… ein Histogramm mit Normalkurve der Variablen iq! Selektieren Sie nun alle Kinder der 7. Klasse und erzeugen Sie auch für diese ein Histogramm mit Normalkurve der Variablen iq! Vergleichen Sie die beiden Grafiken: Je größer die Stichprobe, desto besser die Approximation. Aber die Voraussetzung der Normalität ist für beide Stichproben erfüllt (und wäre es, egal wie die Histogramme aussähen), da IQ "in der Natur" eine normalverteilte Variable ist. Die genaue Verteilung der beobachteten Werte einer Stichprobe ist irrelevant.

Zusammenfassend: Die (parametrische) Statistik setzt gar nicht voraus, dass beobachtete Daten perfekt mit einer Normalverteilung übereinstimmen, sondern lediglich, dass die Variable in der Bevölkerung, aus der wir Stichproben ziehen, normalverteilt ist. Und das ist sowohl mit dem IQ als auch mit einer Fülle von anderen reellen Variablen der Fall. Mehr muss man nicht wissen: Ein Test der Normalität ist bei solchen Variablen redundant (und oft irreführend). (Es gibt trotzdem Fälle, wo die Normalität überprüft werden sollte: Tests dafür werden später genauer besprochen.)

Auch bei zwei der häufigsten Fragebogen-Items kann oft von einer Normal- oder zumindest von einer symmetrischen Verteilung ausgegangen werden:

Semantische-Differential-Skalen

Bei diesen symmetrischen, bipolaren Fragen gibt man an, welcher Begriff (hier von sympathisch bis unsympathisch) das Objekt besser beschreibt:

Hier kann man meistens von einer Normalverteilung ausgehen.

Likert-Skalen

Bei diesen unipolaren Fragen wird zum Beispiel gefragt, wie gut ein Begriff (hier: sympathisch) ein bestimmtes Objekt beschreibt:

Hier kann man ohne Überprüfung NICHT von einer Normalverteilung ausgehen.

Beschreibende Statistiken zur Normalität

Übung:

Öffnen Sie die Datei data.sav. Mittels Analysieren + Mittelwerte vergleichen + Mittelwerte… vergleichen Sie die beiden Geschlechter anhand der Variablen englisch! Lassen Sie dabei über Optionen… folgende Statistiken ausgeben:

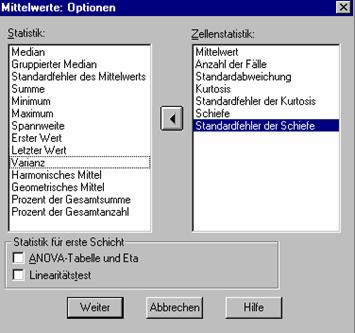
Eine perfekte Normalverteilung ist (unter anderen Eigenschaften) symmetrisch um den Mittelwert. Die Streuung um diesen Mittelwert wird durch die Angabe der Varianz bzw. der Standardabweichung wiedergegeben. Die Angabe des Mittelwerts allein (ohne Standardabweichung) ist meist sinnlos – und auf jeden Fall dann, wenn Mittelwerte verglichen werden sollen.

Übung:

Um dies zu verdeutlichen:

1. Splitten Sie (mittels Daten + Datei aufteilen) die Datei nach Geschlecht.
2. Erzeugen Sie Histogramme mit Normalkurve der Variablen englisch (zur Erinnerung: Analysieren + Deskriptive Statistiken + Häufigkeiten… und Diagramme… ). Edieren Sie beide Grafiken so, dass die Skala der X-Achse von 0.5 bis 15.5 in 15 Schritten dargestellt wird:

Der (intuitive) Eindruck der resultierenden Grafiken

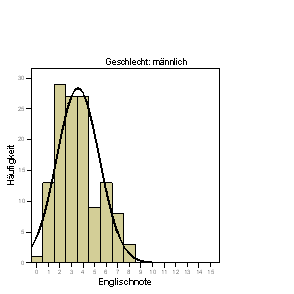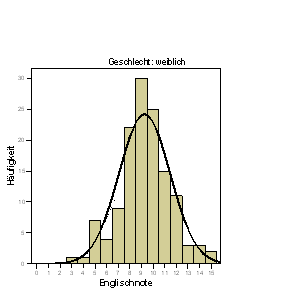ist der, dass die Mädchen eine deutlich bessere Englischnote als die Jungen erreicht haben, denn diese beiden Verteilungen überlappen sich wenig. Es ist u.a. genau dieser Grad der Überlappung, der numerisch erst durch die Angabe der Streuung beider Verteilungen deutlich wird, der uns sagt, ob die beiden Mittelwerte unterschiedlich sind oder nicht. Die beiden Mittelwerte allein sind in diesem Zusammenhang nicht ausreichend. Der passende statistische Test der Hypothese "Mädchen haben besser Englischnoten als Jungen" zieht natürlich auch (und gerade) die Varianzen der beiden Gruppen in Betracht.

Übung:

Testen Sie mittels dem T-Test für unabhängige Stichproben, ob die Mädchen unserer Stichprobe tatsächlich eine bessere Englischnote erhalten haben!

Schiefe beschreibt, inwieweit die beobachtete Verteilung von der Symmetrie einer Normalverteilung abweicht: Schiefe = 0 heißt: keine Abweichung. Ein positiver Werte bedeutet, dass die Verteilung zu weit nach rechts gezogen ist (rechts schief), ein negativer zu weit nach links (links schief).

Kurtosis beschreibt, inwieweit die Verteilung zu spitz (Kurtosis negativ) oder zu flach (Kurtosis positiv) ist. Ein Wert von 0 heißt: Kein Unterschied zu der Gauß'chen Kurve.

Wie groß diese Werte sein müssen, um eine bedeutende Abweichung von der Normalität zu erreichen, errechnet sich aus dem Verhältnis des Wertes (Schiefe bzw. Kurtosis) zu dessen Standardfehler. Traditionsgemäß wird die Normalität bei Werten dieser Verhältnisse größer 2 (bzw. kleiner -2) nicht akzeptiert.

Der relevante Teil der Ausgabe des obigen Mittelwerte-Aufrufs (über die OLAP-Steuerung etwas umformatiert) für die Gesamtstichprobe

erlaubt uns zu berechnen: -1,011 / 0,299 = -3.381 (für Kurtosis) und 0,167 / 0,150 = 1,113 (für die Schiefe).

Der Kurtosis-Wert ist deutlich zu hoch, sodass wir auf dieser Basis das Vorliegen einer Normalverteilung in diesem Fall ablehnen würden. Allerdings sind diese Werte keine ausreichenden Indizien für die Normalität – dafür wurde der unten beschriebene Lilliefors-Test konzipiert. (Übrigens: Die Englischnote wurde simuliert – die Werte stammen tatsächlich aus einer Normalverteilung.)

Statistische Tests

Der Kolmogorov-Smirnov-Test

… wird oft zum Überprüfen der Normalität einer Verteilung herangezogen – aber Vorsicht! Der Test vergleicht eine vorliegende Verteilung mit einer Normalverteilung unter der Annahme, dass die Populations-Streuung und -Mittelwert bekannt sind. Dies ist selten der Fall: Üblicherweise müssen die Parameter anhand der vorliegenden Daten geschätzt werden. Vorsicht auch bei der Interpretation: Ein signifikanter Wert bedeutet, dass die Hypothese der Normalität nicht akzeptiert werden kann.

Die Lilliefors-Korrektur

… zum Kolmogorov-Smirnov-Test (vielmehr: zur Berechnung des Signifikanzniveaus) ist für solche Datensätze geeignet, anhand von denen die Populationsparameter (Mittelwert, Streuung) geschätzt werden müssen (dies ist in den meisten Studien der Fall). Auch hier bedeutet ein signifikantes Ergebnis eine signifikante Abweichung von der Normalität.

Übung:

Wenden Sie diesen formalen Test bei der Englischnote an! Vergleichen Sie dieses Ergebnis mit obigen Berechnungen des Kurtosis-Werts!

Der Shapiro-Wilk-Test

… ist auch für die Situation konzipiert, bei welcher die Parameter aus den vorhanden Daten geschätzt werden müssen. Und auch hier bedeutet Signifikanz, dass Ihre Daten nicht als aus einer Normalverteilung stammend betrachten werden können.

Übung:

Was sagt der Lilliefors-Test auf der Basis der Gesamtstichprobe zu der Frage, ob die Variable iq aus einer Normalverteilung stammen könnte? Wenden Sie denselben Test bei den Kindern der 7. Klasse an!

!Tipp

Vorsicht! Wie bei allen statistischen Tests hängt die Signifikanz auch von der Stichprobengröße ab. Bei größeren Stichproben (Faustregel: ab 50) können kleine und inhaltlich völlig unbedeutsame Abweichungen von der Normalität zur formalen Signifikanz führen. Solche Tests sind in der Praxis kaum brauchbar.

Grafische Darstellungen zur Normalität

Box-Plots

Übung:

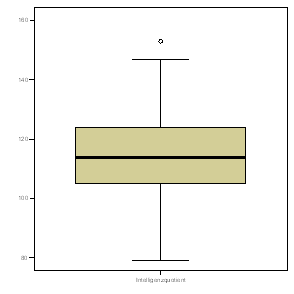
Erzeugen Sie ein Boxplot der Variablen iq für die gesamte Stichprobe und für die Kinder der 7. Klasse!

Verteilung des IQ: Gesamtstichprobe	Verteilung des IQ: 7. Klasse

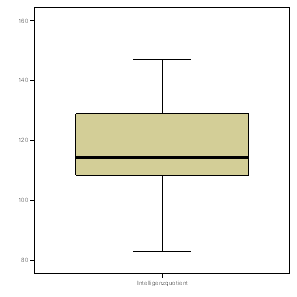Zur Erinnerung: Der IQ ist per definitionem normalverteilt (und wurde in diesem Datensatz auch so simuliert). Fazit: Bei einer Normalverteilung, je größer die Stichprobe, desto symmetrischer wird die Verteilung der beobachteten Werte. Das heißt unter anderem: Eine asymmetrische Verteilung ist noch lange kein Indiz dafür, dass die Variable in der Gesamtbevölkerung nicht normalverteilt wäre.

Histogramm + Normalkurve

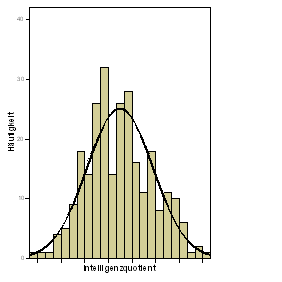
Dieselbe Bemerkung gilt auch für die Histogramm-Darstellung:

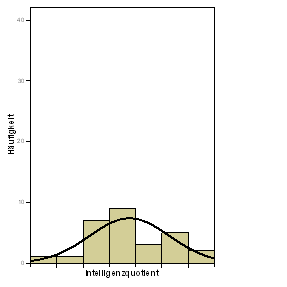
Verteilung des IQ: Gesamtstichprobe	Verteilung des IQ: 7. Klasse

Übung:

Erzeugen Sie ein Histogramm der Variablen iq für die gesamte Stichprobe und für die Kinder der 7. Klasse! Vergleichen Sie die numerischen Werte mit den Grafiken! Vergleichen Sie die Box-Plots mit den Histogrammen!

Normalverteilungs-Plots

Auch die klassischen Grafiken zur Normalverteilung bestätigen unsere Bemerkung: Auch eine (in der Bevölkerung) normalverteilte Variable kann bei kleineren Stichproben besonders deutlich von der perfekten Gauß'schen Kurve abweichen.

Übung:

Mittels Analysieren … Deskriptive Statistiken … Explorative Datenanalyse untersuchen Sie, ob für die beiden Geschlechter getrennt die Variable englisch als normalverteilt betrachtet werden kann! (Zur Erinnerung: Benutzen Sie geschl als Faktor!) Schalten Sie dabei die Statistik-Ausgabe aus, die Plots ein, die Stengel-Blatt Darstellung aus! Schalten Sie Normalverteilungsdiagramm mit Tests ein!

Hier ein Teil der Ausgabe für die männlichen Befragten:

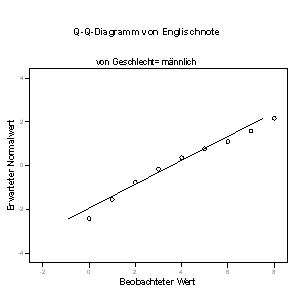
Diese Grafik zeigt Abweichungen von einer normalen Kurve, vor allem in den Extrembereichen.

Ob solche Abweichungen von statistischem Belang sind, kann mit dafür geeigneten Tests überprüft werden: Hier bestätigt der Lilliefors-Test diesen visuellen Eindruck:

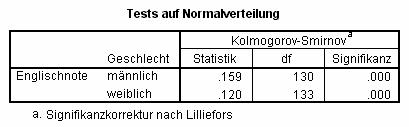
!Tipp:

Dieser Test prüft, ob die Daten in Ihrem Datensatz aus einer Verteilung stammen könnte, die signifikant nicht-normalverteilt ist – d.h. man möchte üblicherweise kein signifikantes Ergebnis dieses Tests vorfinden. Es ist üblich, den Wert 0,1 als Grenzwert für diesen Test zu nehmen: Ist die Signifikanz des Lilliefors-Tests > 0,1, so wird die Annahme der Normalität akzeptiert; ist sie < 0,1 wird die Normalität nicht angenommen.

Siehe auch den Tipp im vorgehenden Kapitel "Statistische Tests".

Wie wichtig ist es, dass diese Voraussetzung der Normalität erfüllt wird?

• "Power"
  Die "Power" eines Tests ist die Wahrscheinlichkeit, signifikante Testergebnisse zu erhalten. Diese ist etwas höher bei parametrischen als bei nicht-parametrischen Tests.
• Korrelation
  Als Maß des linearen Zusammenhangs (Pearson-Korrelationskoeffizient) sind keine Voraussetzungen bezüglich Normalität notwendig. Erst der Test der Signifikanz setzt eine Normalverteilung voraus!
• Varianzanalyse, T-Test
  Parametrische varianzanalytische Verfahren einschließlich des T-Tests setzen zwar die Normalität der zu untersuchenden Variablen voraus, sind jedoch "robust gegenüber Abweichungen von der Normalität" (ein Satz, den man in vielen Arbeiten zitieren kann!).

Was tun, wenn die Voraussetzung der Normalität nicht erfüllt ist?

1. Transformieren

Schief verteilte Variablen können oft mit einer einfachen Transformation symmetrisiert werden.

Beispiel:

Starten Sie SPSS mit einem leeren Datenfenster; oder bei schon aktivem SPSS kreieren Sie über Datei + Neu + Daten ein solches.

Folgender Syntax-Befehlssatz erzeugt 1000 Fälle, jeweils mit drei Variablen:

   input program.
      loop #i = 1 to 1000.
         compute x = rv.normal(100,15).
         compute x2 = x**2.
         compute xm2 = sqrt(x).
         end case.
      end loop.
      end file.
   end input program.
   execute.

Dabei stammen die simulierten x-Werte aus einer Normalverteilung (Mittelwert 100, Standardabweichung 15). Die Variablen x2 und xm2 enthalten x zum Quadrat bzw. Wurzel(x)

Mittels Analysieren + Deskriptive Statistiken + Häufigkeiten analysieren Sie die Verteilung dieser drei Variablen (schalten Sie dabei die Häufigkeitstabelle aus)! Über den Statistik-Knopf wählen Sie Schiefe!

Das Ergebnis: x ist symmetrisch (Schiefe um 0); x2 ist rechts schief (positive Schiefe); xm2 ist links schief (negative Schiefe). Es folgt also: Ist eine Verteilung rechts schief, so könnte eine Wurzeltransformation, ist sie links schief, so könnte eine Quadrierung sie symmetrisieren.

Erzeugen Sie ein Histogramm mit Normalkurve dieser drei Variablen!

2. Nichtparametrische Verfahren anwenden

Nichtparametrische Tests setzen keine vorgegebene Verteilung der zu untersuchenden Variablen voraus, sind aber etwas "schwächer" im Finden von Signifikanz, das heißt: Die Power von nichtparametrischen ist niedriger (allerdings nur geringfügig) als die parametrischer Tests.

Zum Begriff "Signifikanz"

Hypothesen: H₀ und H₁

Der Sinn eines statistischen Tests ist es, Hypothesen zu prüfen. Man spezifiziert zunächst die Null-Hypothese (H₀), dass es keinen (statistischen) Effekt (z.B. keinen Gruppenunterschied) gibt. Die alternative Hypothese (H₁) spezifiziert die zu testende Frage (z.B. dass ein Gruppenunterschied besteht). Eine Teststatistik wird mit einem passenden Verfahren berechnet: Unter der Grundannahme, dass die Null-Hypothese stimmt, wird gefragt, wie wahrscheinlich es ist, eine Teststatistik zu H₁ zu erhalten, die größer (extremer) ist, als die erhaltene: Dieser Wert ist die Signifikanz.

Ein wichtiger Grundsatz der angewandten Statistik lautet: H₁ – explizit nicht H₀ – wird getestet! Das heißt: Man kann gar nicht testen, ob kein Unterschied vorliegt. Dies hat weit reichende Konsequenzen. Beispiel: Ein Mediziner möchte die Wirkung zweier Medikamente vergleichen, die den diastolischen Blutdruck senken sollen. Er teilt seine Patientenstichprobe in zwei Gruppen: Die eine erhält das erste, die andere das zweite Medikament. Nun möchte unser Mediziner sicher sein, dass kein Gruppenunterschied  schon vor Applikation der Medikamente vorliegt. Er möchte also die Null-Hypothese testen, die jedoch gar nicht testbar ist. Folgen wir der Logik dieses Beispiels weiter: Fände unser Mediziner einen signifikanten Ausgangs-Unterschied zwischen den beiden Gruppen, so müsste er diesen beim Testen der Experimentalunterschiede explizit in Betracht ziehen (eine Kovarianzanalyse wäre hier angebracht). Fände er aber keinen signifikanten Ausgangs-Unterschied, so hieße dies noch lange nicht, dass es überhaupt keinen Unterschied gäbe und vor allem nicht, dass mögliche Ausgangsunterschiede die Experimentalergebnisse nicht hätten beinflussen können. Auch hier wäre eine Kovarianzanalyse angebracht, die die Ausgangs-Blutdruckwerte explizit in Betracht zieht – effektiv werden dabei die Ausgangs-Blutdruckwerte der beiden Gruppen statistisch-mathematisch ausgeglichen, bevor die Experimentalunterschiede untersucht werden.. Anders gesagt: Der Test der Experimentalunterschiede wird von möglichen Ausgangsunterschieden "bereinigt". (Präziser: es wird für den linearen Anteil dieser Ausgangswerte korrigiert.)

Signifikanz intuitiv

Etwas anschaulicher ausgedrückt: Die Wahrscheinlichkeit sagt, wie die Lage in der reellen Welt ist. Hätte man zum Beispiel einen signifikanten (p< 0.01) Unterschied in den mittleren Berufsschancen von Mädchen und Jungen bei einer Stichprobe gefunden, so könnte man mit 99% [= (1-p) × 100] Sicherheit behaupten, bei allen Schülern der untersuchten Bevölkerung bestünde der Unterschied auch. Die formal korrekte – und wichtigste – Formulierung: Diese Wahrscheinlichkeit ist die Chance, dass die beobachteten Ergebnisse per Zufall entstanden sind, also: Zufällig bei dieser Stichprobe beobachtet wurden, jedoch in der Bevölkerung nicht vorhanden sind.

Auch hier eine Anmerkung: Kein statistischer Test kann eine Hypothese mit 100% Sicherheit bestätigen: Das geht nur dann, wenn die gesamte Bevölkerung untersucht wird; und hätte man die gesamte Bevölkerung, so bräuchte man gar keine statistische Schätzung, wie die Lage in dieser Bevölkerung ist – man wüsste es ja.

Einseitige und zweiseitige Hypothesen

In unserem Beispiel zur Variablen chancen ist die Hypothese nicht nur "gibt es einen Unterschied?": Wir spezifizieren auch die Richtung dieses Unterschieds. Wir wollen gezielt testen, ob Schüler einen höheren Mittelwert aufweisen als Schülerinnen – ist der Mittelwert der Schüler niedriger als der der Schülerinnen, dann ist die Sache schon ohne statistischen Test erledigt. Eine solche Hypothese nennt man "einseitig". Interessieren wir uns dagegen lediglich dafür, ob es überhaupt einen Unterschied gibt, unabhängig davon, welche Gruppe den höheren Mittelwert geliefert hat, so heißt diese Variante eine "zweiseitige" Hypothese.

Der p-Wert: Signifikanz

Signifikanz (p) wird als Wahrscheinlichkeit augedrückt: 0 ≤ p ≤ 1 (0 heißt: kann auf keinen Fall passieren; 1 heißt: passiert auf jeden Fall). Der Begriff Signifikanz bedeutet: Wie hoch ist die Wahrscheinlichkeit, dass ich meine Ergebnisse falsch interpretiere? Oder aber auch: Wie sicher kann ich sein, dass meine Ergebnisse auf die reelle Welt übertragbar sind?

Dabei werden zwei Arten von Fehlentscheidungen unterschieden:

Fehler Typ I

Verwirft man die Null-Hypothese, obwohl sie eigentlich korrekt ist, dann macht man einen so genannten Fehler Typ I. Anders gesagt: man "findet" einen Unterschied, der per Zufall in dieser Stichprobe vorkam, aber in der Bevölkerung gar nicht existiert.

Fehler Typ II

Akzeptiert man die Null-Hypothese, obwohl sie eigentlich falsch ist, dann macht man einen Fehler Typ II: Es ist ein Unterschied vorhanden, aber man findet ihn nicht.

Es bleibt die grundsätzliche Frage: Was für p-Werte sind akzeptabel?

Der Alpha-Wert

Bevor man eine Studie unternimmt, setzt man den Signifikanzwert fest, der erreicht werden muss, um die Nullhypothese zu verwerfen. Dieser Wert wird als Alpha bezeichnet. Traditionsgemäß wird häufig einen Alpha-Wert von 0,05 gewählt. Das bedeutet: "Ich akzeptiere ein Risiko von 5% (100 × 0,05), dass ich einen Fehler Typ I mache" (d.h.: "Signifikanz" finde, die rein per Zufall in meiner Stichprobe vorkommt, die aber sonst gar nicht existiert).

5% Risiko mag in Studien akzeptabel sein, wo Messfehler gering bzw. die Konsequenzen eines Fehlentschlusses nicht allzu wichtig sind. In anderen Fällen sind Werte von 0,01 (1% Risiko eines Fehlers), 0,001 (0,1% Risiko) oder gar noch kleiner angemessen und in seriösen Publikationen durchaus üblich.

Die Effektgröße (Relevanz versus Signifikanz)

Der Effekt spiegelt die zu testende Hypothese wider – Beispiele:

• unterscheidet sich ein beobachteter Korrelationskoeffizient von Null?
• unterscheiden sich Gruppen-Mittelwerte?
• unterscheidet sich die Steigung einer Regressionsgerade von Null?

Diese Effektgröße legt den kleinsten akzeptablen Effekt fest. Die in der Praxis relevante Größe eines solchen Effekts hängt von der jeweiligen Anwendung ab: Bei einer kleinen Pilotstudie, die lediglich festzustellen versucht, ob die Geschlechter sich anhand einer Variablen unterscheiden könnten, könnte die gewünschte Effektgröße relativ klein sein; bei einer Untersuchung, ob ein teueres und schmerzhaftes Operationsverfahren besser als ein herkömmliches Verfahren ist, würde man einen deutlich größeren Effekt verlangen. Die Effektgröße legt den kleinsten akzeptablen Effekt fest.

Signifikante Ergebnisse heißen noch lange nicht, dass sie in der Praxis von Bedeutung sind!

Beispiel:

Man habe zwischen zwei Variablen anhand von 10.000 Probanden einen Pearson-Korrelationskoeffizienten r von 0,03, p < 0,01. Mit 99% Sicherheit ist dieser Koeffizient "echt" – existiert also in der Bevölkerung. Der Wert 100×r² gibt den prozentualen Anteil der gemeinsamen Varianz zwischen den beiden Variablen wieder: in diesem Fall also 0,09%. Das Signifikanzniveau mag theoretisch interessant sein, ist aber für praktische Zwecke kaum von Bedeutung: Etwas salopp ausgedrückt: Mehr als 99% der einen Variablen hat nichts mit der anderen zu tun!

Ein deutliches Warnzeichen kann schon eine hohe Stichprobengröße sein, denn Signifikanz hängt nicht nur von der Effektgröße (hier: Grad der Korrelation), sondern unmittelbar auch von der Stichprobengröße ab. Mit einer genügend großen Stichprobe wird auch ein winziger Effekt signifikant – das heißt: Dieser winzige Effekt ist (mit einer gewissen Wahrscheinlichkeit) reell. In der Praxis wichtig ist und bleibt letztendlich jedoch die Größe dieses Effekts. Und wie groß bei Ihrer Untersuchung dieser sein muss können nur Sie aus inhaltlichen Gründen bestimmen.

Übung:

Bestimmen Sie über Analysieren… Korrelation … Bivariat den Pearson'schen Korrelationskoeffizienten zwischen chancen und beruf!

Wie viel Varianz (in Prozent ausgedrückt) haben die beiden Variablen gemeinsam?

Beispiel: R²

Das quadrierte multiple R enthält ähnliche Informationen z.B. bei einer linearen Regression; nämlich den Anteil der Varianz der abhängigen Variablen, der durch die unabhängigen Variablen erklärt wird.

Beispiel: Eta quadriert

Bei der Varianzanalyse gibt die Statistik "eta-quadriert" die Proportion der Varianz der abhängigen Variablen wieder, die durch die Gruppenunterschiede erklärt werden kann. Wie bei r² und R² spiegelt dies eine Art praktische Relevanz wider: Man kann auch hier mit einer großen Stichprobe ein hohes Niveau an Signifikanz bei einem kleinen Effekt erreichen, der in der Praxis kaum von Bedeutung sein könnte.

Übung:

Erzeugen Sie (über Grafiken) ein Scattergramm mit Y-Achse chancen, X-Achse beruf! Erzeugen Sie die lineare Regressionslinie dazu!

Über Analysieren … Regression erzeugen Sie die statistische Analyse zu Ihrer Grafik!

Interpretieren Sie die Statistiken: Kann man anhand des Wertes beruf Brauchbares über die Höhe des Wertes chancen schließen?

Präzision und Konfidenzintervalle

Ein Effekt wird typischerweise anhand von Daten geschätzt: Untersucht man zum Beispiel zwei Gruppenmittelwerte (und natürlich die Streuung), so wird der statistische Test gewöhnlich auf der Basis von Schätzungen dieser Mittelwerte durchgeführt.

Oft will man jedoch eine bestimmte (Mindest-)Effektgröße erreichen. Beispiel aus dem Bereich Medizin: Ein neues Medikament soll getestet werden, der hohe diastolische Blutdruckwerte gezielt senken soll. Die Forscher interessieren sich nicht für kleinere, für die Praxis irrelevante Änderungen, sondern verlangen eine Senkung um mindestens 15 Punkte. Somit rückt die Präzision der Schätzung des Effekts in den Vordergrund. Diese Präzision wird anhand vom Konfidenzintervall dargestellt. So berichtet man etwa: "Das Medikament senkte mit 95% Sicherheit die Werte um 10 (± 3) Punkte".

Bei vielen statistischen Tests gibt SPSS diese Konfidenzintervalle aus, so zum Beispiel beim T-Test (hier ein Teil der Ausgabe):

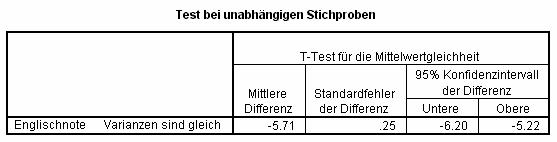
Geschlechtsunterschiede (männlich minus weiblich) anhand der Englischnote wurden untersucht. Im Schnitt liegt diese Differenz bei -5,71 Punkten (Schülerinnen sind im Schnitt knapp 6 Punkte besser als Schüler). Mit 95% Sicherheit liegt die "wahre" (Bevölkerungs-)Differenz zwischen den Konfidenzintervallen -6,20 und -5,22 – gerundet also: zwischen 5 und 6 Punkten.

Power-Analyse

Power

Die "Power" eines Tests ist die Wahrscheinlichkeit, dass die Ergebnisse (p-Werte) einer statistischen Analyse den vorgegebenen Alpha-Wert erreichen werden. Anders formuliert: Power ist die Wahrscheinlichkeit, signifikante Ergebnisse zu erhalten. Traditionsgemäß wird Power mit 0,80 festgelegt, was wiederum bedeutet, dass die Wahrscheinlichkeit eines Fehlers Typ II (1,00 – 0,80 =) 0,20 beträgt. Mit einem Alpha von beispielsweise 0,05 bedeutete dies nun, dass ein Fehler Typ I (0,20 / 0,05 =) 4 mal so schädlich wäre als ein Fehler Typ II. Offensichtlich müssen solche Überlegungen von Studie zu Studie neu, mit großer Vorsicht und intimen Kenntnissen der möglichen Konsequenzen einer Fehlentscheidung gemacht werden. Es reicht auf keinen Fall, Werte wie Alpha = 0,05 und Power = 0,80 für eine Studie zu übernehmen, nur weil diese Werte Tradition haben.

Die Effektgröße, die Stichprobengröße, der Alpha-Wert und Power bilden zusammen ein "geschlossenes System" – kennt man die Werte drei dieser Parameter, so ist der vierte komplett definiert. Hierzu einige Hinweise:

• je größer der Effekt, desto kleiner braucht die Stichprobe zu sein, um den gewünschten Alpha-Wert zu erreichen;
  und umgekehrt:
• je größer die Stichprobe, desto kleiner der Effekt, der den gewünschten Alpha-Wert liefert (wobei sich wieder die Frage der Relevanz stellt: Ist ein so kleiner Effekt überhaupt von praktischer Relevanz?);
  das heißt auch:
• je größer die Stichprobe, desto größer auch die Power;
  und:
• je kleiner der Alpha-Wert, desto kleiner die Power. Desto unwahrscheinlicher ist es also, einen Fehler Typ I (Signifikanz "finden", die nicht existiert) zu machen – dafür steigt jedoch die Wahrscheinlichkeit eines Fehlers Typ II (eine existierende Signifikanz nicht zu entdecken).

Diese Kenntnisse erlauben uns zum Beispiel bei einer gewünschten Effektgröße (bekannt etwa durch unsere inhaltlichen Kenntnisse der Materie oder aus einer Pilotstudie) und akzeptablen Alpha und Power-Werten (festgelegt nach den schon beschriebenen Überlegungen) zu fragen: Wie groß muss die Stichprobe sein, um Signifikanz zu erreichen?

Das Programm 'Sample Power'

Das Programm Sample Power von der Firma SPSS (das auch Teil der LRZ-SPSS-Lizenz ist) unterstützt solche Power-Analysen. Die Eingabe besteht aus Parameter-Werten wie Effektgröße, Alpha und Power; Ausgabe zum Beispiel aus der benötigten Stichprobengröße; aber auch aus (englischsprachigem) Klartext, der unmittelbar in einer Arbeit eingebaut werden kann.

Beispiel:

Anhand einer Pilotstudie kennen wir die IQ-Mittelwerte (115 bzw. 123) von zwei Berufsgruppen: Die (Bevölkerungs-)Streuung des IQs ist per definitionem 15. Wir wollen mittels des T-Tests diesen Unterschied (123 - 115 =) 8 auf Signifikanz testen; und wollen schätzen, wie groß die Stichprobe dafür sein müsste.

Der Test ist zweiseitig (2-Tailed): Wir wollen lediglich wissen, ob die zwei Gruppen sich unterscheiden, nicht ob die zweite Gruppe höhere Werte hat.

Das Programm Sample Power setzt per Voreinstellung die Werte Alpha = 0,05, Power = 80% und Tails = 2 (Diese Werte, sowie die Effektgröße (8) können selbstverständlich vom Anwender geändert werden): Das Ergebnis der Analyse mit diesen Parametern:

Um mit mindestens 80% Wahrscheinlichkeit einen signifikanten (Alpha = 0,05) Unterschied zwischen den beiden Gruppen für diese Variablen zu finden wäre eine Stichprobe von 57 pro Gruppe notwendig. Das Programm gibt auch folgende Kurzbeschreibung aus:

"Capitalizing on Chance"

Dieser Ausdruck beschreibt eine häufige Falle der Anwendung des Signifkanz-Niveaus: Je mehr Tests man untersucht, desto größer ist die Chance, Signifikanzen zu finden, die lediglich per Zufall entstanden sind. Etwas einfach ausgedrückt: Führt man 100 Tests mit einem Alpha-Wert von 0,05 durch, so sind 5% dieser Tests rein zufällig signifikant (welche 5% weiß man nicht – daher die Gefahr). Es wäre auf jeden Fall völlig falsch und verantwortungslos, alle möglichen Tests mit Ihren Daten durchzuführen, die anscheinend "signifikanten" Ergebnisse auszuwählen und diese dann so darzustellen, als ob sie Ihren ursprünglichen Hypothesen entsprächen. Der korrekte Vorgang: Hypothesen generieren, bevor Sie die Daten inspizieren und analysieren (üblicherweise sogar bevor Sie die Daten überhaupt sammeln) und diese Hypothesen dann gezielt testen. Capitalizing on Chance ist das bewusste oder unbewusste Ignorieren dieser Gefahr, das Berichten also von irrtümlich "signifikanten" Ergebnissen, die gar nicht signifikant sind. Tut man dies mit Absicht, dann kann das nur als Schwindel bezeichnet werden.

Alpha-Fehler-Kumulierung

Je mehr Tests durchgeführt werden, desto "überhöhter" sind die üblichen Signifikanzangaben. Mit einem einzigen Test und einem Alpha von 0,05 ist die Wahrscheinlichkeit, die Null-Hypothese korrekterweise zu akzeptieren (1 - 0,05) = 0,95. Führen wir zwei (unabhängige) Tests durch, so wird diese Wahrscheinlichkeit deutlich reduziert: 0,95² = 0,90, was eine ebenso deutliche Änderung des entsprechenden Alpha-Werts von 0,05 auf 0,1 bedeutet. Diese Fehlerquelle ist allgemein als Alpha-Fehler-Kumulierung bekannt.

Beispiel:

Über Analysieren + Korrelation + Bivariat… berechnen Sie die Pearson'sche Korrelation mit zweiteiligem Signifikanztest zwischen den Variablen deutsch, mathe, englisch, iq und chancen. Das Ergebnis:

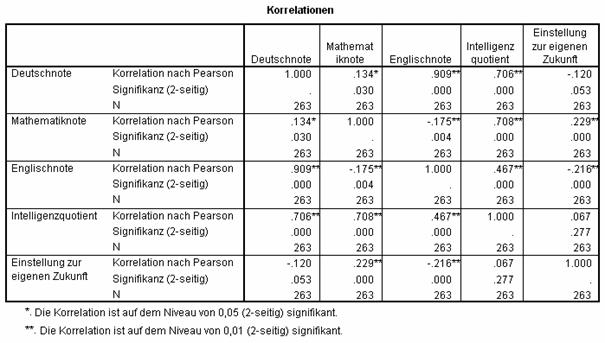
Schon diese fünf Variablen führen zu ½n(n - 1) = 10 Korrelationskoeffizienten und 10 damit verbundenen Signifikanztests. Mit einem Alpha von 0,05 ist nun die Wahrscheinlichkeit, H₀ korrekterweise zu akzeptieren nur noch (1 - 0,05)¹⁰ = 0,60 mit einem entsprechenden, veränderten und völlig unakzeptablen Alpha von 0,40. Dieser Gedanke führt zur einfachen Bonferroni-Korrektur: Man multipliziere das einfache Signifikanzniveau p mit der Anzahl Tests. Liegen diese so veränderte Signifikanz-Werte immer noch unter dem ursprünglichen Alpha (hier: 0,05), so können als signifikant betrachtet werden. Es ist bedauerlich, dass SPSS diese Korrektur als Option nicht anbietet.

Um diese Bonferroni-Korrektur anzuwenden, müssen also die Signifikanzwerte mit der Anzahl Tests – hier (5 × 4 /2)=10 – multipliziert werden. Vorsicht bei dieser Berechnung: Es geht nicht um die Anzahl Variablen n, die Untersucht werden, sondern um die Anzahl durchgeführte Tests (=berechnete Koeffizienten)! Vor allem wird im obigen Beispiel die Korrelation zwischen den Mathe- und Deutschnoten betroffen. Der tabellierte, unkorrigierte p-Wert beträgt 0,03, der korrigierte Wert 0,3: mit Alpha = 0,05 (fälschlicherweise) signifikant vor der Korrektur, (korrekterweise) nicht signifikant danach.

Exakte Tests: Das Problem der kleinen Stichproben

Auch nichtparametrischen Tests liegen gewisse Verteilungsannahmen zugrunde – zwar nicht für die abhängigen Variablen selber, aber sehr wohl für die berechneten statistischen Werte (zum Beispiel für die Mann-Whitney-U-Statistik): Es wird angenommen, dass mit genügend zugrunde gelegten Rohdaten ("asymptotisch") die zu erwartende Verteilung der Teststatistik gegeben ist, sodass der berechnete Wert mit dieser theoretischen Verteilung verglichen werden kann. Was genau jedoch "genügend" ist, weiß keiner: Bei kleineren oder unbalancierten Stichproben sind diese Voraussetzungen jedenfalls meist nicht erfüllt.

Übung:

Öffnen Sie die Datei .data2.sav. Mittels Daten … Fälle auswählen selektieren Sie Kinder der 13. Klasse! Mit Analysieren … Deskriptive Statistiken … Kreuztabellen erzeugen Sie eine Kreuztabelle der Variablen geschl und schultyp! Schalten Sie die Chi-Quadrat-Statistik ein!

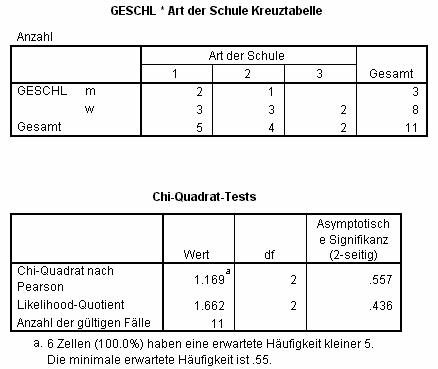
Zur Interpretation:

Der erste Teil der Ausgabe enthält eine einfache Kreuztabelle: Die Zellen enthalten die Anzahl Fälle, die zur jeweiligen Kombination der Ausprägungen der analysierten Daten gehören. So besuchen z.B. drei Schülerinnen den Schultyp 2. Die Randwerte enthalten die Summen der jeweiligen Ausprägungen: 3 Schüler und 8 Schülerinnen sind in dieser Tabelle zusammengefasst.

Der zweite Teil der Ausgabe enthält unter anderem den Pearson'schen Chi-Quadrat-Test, der die Unabhängigkeit der beiden Variablen geschl und schultyp testet: Ist dieser Wert signifikant, so sind die beiden Klassifizierungen nicht voneinander unabhängig: Gäbe es z.B. eine klare Präferenz der Schülerinnen für einen bestimmten Schultyp, so wäre diese Statistik signifikant.

Der dritte Teil der Ausgabe enthält eine deutliche Warnung, dass die Voraussetzungen für den asymptotischen Test nicht erfüllt sind.

Übung:

Wiederholen Sie die Analyse, schalten Sie aber über den Knopf Exakt das Monte-Carlo-Verfahren ein! Vergleichen Sie die vorherigen und die neuen Signifikanzwerte!

Übungen

1. Öffnen Sie die Datei alcohol.sav !
2. Inspizieren Sie die Liste der Variablen (Hinweis: Dafür gibt es ein Werkzeug!), um ein Gefühl für den Inhalt der Daten zu bekommen!
3. Wenden Sie passende Methoden der beschreibenden Statistik an, um die Daten zusammenzufassen!
4. Benutzen Sie grafische Methoden, um die Normalität der Variablen stre_v und str_n zu untersuchen!
5. Lassen Sie Statistiken (vor allem Kurtosis und Schiefe) zu der Normalität dieser Variablen ausgeben. Bestätigen diese Werte Ihren Eindruck?
6. Wenden Sie einen passenden, formalen statistischen Test an, um die Normalität der beiden Variablen zu überprüfen!
7. Erzeugen Sie eine Grafik, die die Verteilung der beiden Variablen für Stadt- und Landbewohner vergleicht!
8. Berechnen Sie eine neue Variable, die den Unterschied zwischen Stress-Level vor und nach Alkoholeinnahme enthält! Überprüfen Sie, ob dieser neue Wert als normalverteilt betrachtet werden kann!
9. Berechnen Sie die Korrelationen zwischen den beiden Stress-Variablen und Alkoholeinnahme (Pearson oder Spearman? Die Berechnung der Signifikanz bei Pearson beruht auf der Annahme der Normalität, bei Spearman nicht)! Diese Korrelationsmatrix enthält ½n(n - 1) Koeffizienten. Falls Signifikanz berichtet wird, so müssen die berechneten Signifikanz- (p-) Werte nach dem Verfahren von Bonferroni korrigiert werden!
10. Erstellen Sie eine Grafik, die die Korrelation zwischen Alkoholeinnahme und dem Stress-Unterschied vor und nach Alkoholeinnahme darstellt! Berechnen Sie die Spearman'sche Korrelation dazu!
11. Unterscheiden sich Städte von Landbewohnern anhand der Alkoholeinnahme? Stress vor Alkoholeinnahme? Stress nach Alkoholeinnahme? Dem Stress-Unterschied vor und nach Alkoholeinnahme? Das sind drei Tests: Korrigieren Sie die Signifikanzwerte nach dem Verfahren von Bonferroni!
12. Unterscheiden sich Männer von Frauen anhand der Alkoholeinnahme? Stress vor Alkoholeinnahme? Stress nach Alkoholeinnahme? Dem Stress-Unterschied vor und nach Alkoholeinnahme? Auch hier müssen die ausgegebenen Signifikanz-Werte korrigiert werden!
13. Wiederholen Sie den Geschlechtsvergleich, aber veranlassen Sie dabei, dass SPSS auch den Unterschied Stadt/Land berücksichtigt!
14. Falls Sie signifikante Unterschiede finden, erzeugen Sie Grafiken dazu!

Literatur

[1] Bortz, J. (1999) Statistik für Sozialwissenschaftler.  Berlin: Springer-Verlag

[2] Wiseman, M. (2004).  SPSS für Windows: Eine Einführung. München: Leibniz-Rechenzentrum der Bayerischen Akademie der Wissenschaften